At which angle should a thrown ball always fly away from you?

[azatkgz]

Homework Statement

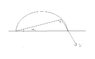
At which angle we should throw the ball ,so it always flies away from you?

The Attempt at a Solution

Somewhere after the max height the velocity of the stone is tangent to the line joining with the starting point(you can look to the file).Let's say that angle of this line with the ground is $$\alpha$$ .So $$\frac{y}{x}=tan\alpha$$ .And i think that stone always goes away when $$\frac{mv^2}{R}\geq mgsin\alpha$$ .Here we can find everything except R.I don't know what to put in it.

 

[learningphysics]

What exactly is the question word for word?

 

[azatkgz]

For example you throw throw the ball up at 90 degrees to ground.It reaches max height and comes back to you.If you throw,let's say,at 80 degrees.At max height it further to you than when it hits the ground.So at some time it went closer to you.

 

[Dick]

Write down x(t) and y(t) for the ball with yourself as the origin. Then the squared distance from you to the ball r(t)=x(t)^2+y(t)^2. If it's coming toward you, then r'(t)<0. So you don't want the expression r'(t)=0 to have any real roots. The problem reduces to showing under what conditions a certain quadratic has no real roots.

 

[azatkgz]

Great!Thanks Dick.I've found
$$sin^2\theta\leq\frac{8}{9}$$

 

[Dick]

Good job. That was fast! I underestimated you. I should have stopped with the first clue.

 

[learningphysics]

Good job. That was fast!

I agree. Nicely done.