- #1
Dmalyuta
- 7
- 0
Hi all,
I'm using Matlab to try and smulate the orbits of Mercury and Venus aroudn the Sun, allowing all three to disturbe each others' orbits.
However, I am constantly running into this problem- all of my orbits look like in the pictures below- in effect, the planets spin out of orbit and will not stay in one ellipse. Even when I Venus out of the equation, mercury still displays this wild behavior.
This is obviosly the result of a problem in the code I've written for this simulation; my question si whether someone could explain to me for what reason such bizarre motion would result (what force is missing, etc.?) so that I can start looking in the right places in my code. For reference, the code I wrote is as follows. For only Sun and Mercury:
For Sun, Mercury, and Venus:
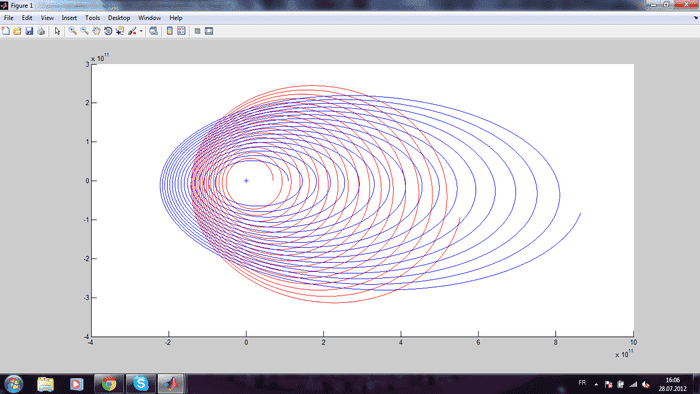
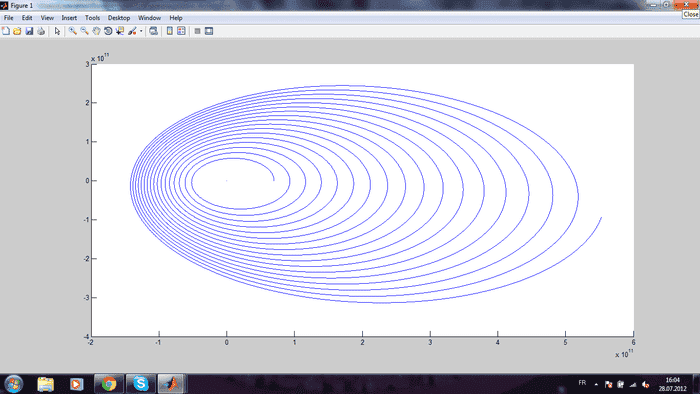
I'm using Matlab to try and smulate the orbits of Mercury and Venus aroudn the Sun, allowing all three to disturbe each others' orbits.
However, I am constantly running into this problem- all of my orbits look like in the pictures below- in effect, the planets spin out of orbit and will not stay in one ellipse. Even when I Venus out of the equation, mercury still displays this wild behavior.
This is obviosly the result of a problem in the code I've written for this simulation; my question si whether someone could explain to me for what reason such bizarre motion would result (what force is missing, etc.?) so that I can start looking in the right places in my code. For reference, the code I wrote is as follows. For only Sun and Mercury:
Code:
% Mapping planet coordinates for 3 bodies- Sun, Mercury, Venus
clear
clf
%% Asking user to input some information and defining some constants
tim=10000;
interva=0.3;
G=6.67384e-11;
%% Sun initial coordinates
M_S=1.989e+30; % mass of sun
x(1,1)=0.0; % x-coordinate. (a,b) where a is the planet number (Sun is #1) and b is the time interval number (1 means time=0s)
y(1,1)=0.0;
V_x(1,1)=0.0; % velocity in x-direction
V_y(1,1)=0.0; % velocity in y-direction
%% Mercury initial coordinates
M_M=3.3e+23; % mass of mercury
x(2,1)=6.98e+10; % note that here a=2, which is mercury's number from the Sun. x-coordinate derived from planet's aphelion
y(2,1)=0.0; % all planets in my simulation start from x-axis
V_x(2,1)=0.0;
V_y(2,1)=38860; % note that all planets start from minimum velocity as such is the case at the aphelion (furthest) position from the sun
%% Venus initial coordinates
M_V=4.87e+24; % mass of venus
x(3,1)=1.09e+11;
y(3,1)=0.0;
V_x(3,1)=0.0;
V_y(3,1)=34790;
%% We now run a loop which will drop out coordiantes of planet positions at different times
timeend=tim*24*3600;
interval=interva*24*3600;
cell=1;
for iter=0:interval:timeend
for i=1:2
switch i
case 1
r_SM=sqrt((x(2,cell)-x(1,cell))^2+(y(2,cell)-y(1,cell))^2);
r_SV=sqrt((x(3,cell)-x(1,cell))^2+(y(3,cell)-y(1,cell))^2);
a_x(1,cell)=-(G*M_M*(x(1,cell)-x(2,cell)))/(r_SM^3);
a_y(1,cell)=-(G*M_M*(y(1,cell)-y(2,cell)))/(r_SM^3);
V_x(1,cell+1)=V_x(1,cell)+interval*a_x(1,cell);
V_y(1,cell+1)=V_y(1,cell)+interval*a_y(1,cell);
x(1,cell+1)=x(1,cell)+interval*V_x(1,cell);
y(1,cell+1)=y(1,cell)+interval*V_y(1,cell);
case 2
r_SM=sqrt((x(2,cell)-x(1,cell))^2+(y(2,cell)-y(1,cell))^2);
r_MV=sqrt((x(3,cell)-x(2,cell))^2+(y(3,cell)-y(2,cell))^2);
a_x(2,cell)=-(G*M_S*(x(2,cell)-x(1,cell)))/(r_SM^3);
a_y(2,cell)=-(G*M_S*(y(2,cell)-y(1,cell)))/(r_SM^3);
V_x(2,cell+1)=V_x(2,cell)+interval*a_x(2,cell);
V_y(2,cell+1)=V_y(2,cell)+interval*a_y(2,cell);
x(2,cell+1)=x(2,cell)+interval*V_x(2,cell);
y(2,cell+1)=y(2,cell)+interval*V_y(2,cell);
end
end
cell=cell+1;
end
hold on
for i=1:2
plot(x(i,:),y(i,:))
end
hold offFor Sun, Mercury, and Venus:
Code:
% Mapping planet coordinates for 3 bodies- Sun, Mercury, Venus
clear
clf
%% Asking user to input some information and defining some constants
tim=10000;
interva=0.3;
G=6.67384e-11;
%% Sun initial coordinates
M_S=1.989e+30; % mass of sun
x(1,1)=0.0; % x-coordinate. (a,b) where a is the planet number (Sun is #1) and b is the time interval number (1 means time=0s)
y(1,1)=0.0;
V_x(1,1)=0.0; % velocity in x-direction
V_y(1,1)=0.0; % velocity in y-direction
%% Mercury initial coordinates
M_M=3.3e+23; % mass of mercury
x(2,1)=6.98e+10; % note that here a=2, which is mercury's number from the Sun. x-coordinate derived from planet's aphelion
y(2,1)=0.0; % all planets in my simulation start from x-axis
V_x(2,1)=0.0;
V_y(2,1)=38860; % note that all planets start from minimum velocity as such is the case at the aphelion (furthest) position from the sun
%% Venus initial coordinates
M_V=4.87e+24; % mass of venus
x(3,1)=1.09e+11;
y(3,1)=0.0;
V_x(3,1)=0.0;
V_y(3,1)=34790;
%% We now run a loop which will drop out coordiantes of planet positions at different times
timeend=tim*24*3600;
interval=interva*24*3600;
cell=1;
for iter=0:interval:timeend
for i=1:3
switch i
case 1
r_SM=sqrt((x(2,cell)-x(1,cell))^2+(y(2,cell)-y(1,cell))^2);
r_SV=sqrt((x(3,cell)-x(1,cell))^2+(y(3,cell)-y(1,cell))^2);
a_x(1,cell)=-(G*M_M*(x(1,cell)-x(2,cell)))/(r_SM^3)+-(G*M_V*(x(1,cell)-x(3,cell)))/(r_SV^3);
a_y(1,cell)=-(G*M_M*(y(1,cell)-y(2,cell)))/(r_SM^3)+-(G*M_V*(y(1,cell)-y(3,cell)))/(r_SV^3);
V_x(1,cell+1)=V_x(1,cell)+interval*a_x(1,cell);
V_y(1,cell+1)=V_y(1,cell)+interval*a_y(1,cell);
x(1,cell+1)=x(1,cell)+interval*V_x(1,cell);
y(1,cell+1)=y(1,cell)+interval*V_y(1,cell);
case 2
r_SM=sqrt((x(2,cell)-x(1,cell))^2+(y(2,cell)-y(1,cell))^2);
r_MV=sqrt((x(3,cell)-x(2,cell))^2+(y(3,cell)-y(2,cell))^2);
a_x(2,cell)=-(G*M_S*(x(2,cell)-x(1,cell)))/(r_SM^3)+-(G*M_V*(x(2,cell)-x(3,cell)))/(r_SV^3);
a_y(2,cell)=-(G*M_S*(y(2,cell)-y(1,cell)))/(r_SM^3)+-(G*M_V*(y(2,cell)-y(3,cell)))/(r_SV^3);
V_x(2,cell+1)=V_x(2,cell)+interval*a_x(2,cell);
V_y(2,cell+1)=V_y(2,cell)+interval*a_y(2,cell);
x(2,cell+1)=x(2,cell)+interval*V_x(2,cell);
y(2,cell+1)=y(2,cell)+interval*V_y(2,cell);
case 3
r_SV=sqrt((x(3,cell)-x(1,cell))^2+(y(3,cell)-y(1,cell))^2);
r_MV=sqrt((x(3,cell)-x(2,cell))^2+(y(3,cell)-y(2,cell))^2);
a_x(3,cell)=-(G*M_S*(x(3,cell)-x(1,cell)))/(r_SM^3)+-(G*M_M*(x(3,cell)-x(2,cell)))/(r_SV^3);
a_y(3,cell)=-(G*M_S*(y(3,cell)-y(1,cell)))/(r_SM^3)+-(G*M_M*(y(3,cell)-y(2,cell)))/(r_SV^3);
V_x(3,cell+1)=V_x(3,cell)+interval*a_x(3,cell);
V_y(3,cell+1)=V_y(3,cell)+interval*a_y(3,cell);
x(3,cell+1)=x(3,cell)+interval*V_x(3,cell);
y(3,cell+1)=y(3,cell)+interval*V_y(3,cell);
end
end
cell=cell+1;
end
hold on
plot(x(1,:),y(1,:),'+')
plot(x(2,:),y(2,:),'r')
plot(x(3,:),y(3,:),'b')
hold off