bwitt
- 3
- 1
- Homework Statement
- Radar readings determine that an object is located at 7,653.76km with a velocity of 3.1621I-2.3716K km/s. Determine p, e, u0, the longitude of ascending node, the argument of periapsis, the true anomaly at epoch, longitude at epoch, and the latitude of impact
- Relevant Equations
- see below
Hello everyone! This is from The Fundamentals of Astrodynamics Chapter 2 Questions. I'm doing this as a self-study (and never took Linear Algebra) so my "technique" might be a little sloppy 

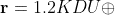
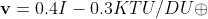
Finding specific angular momentum
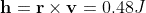
Finding the orbital parameter
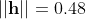
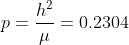
Finding Eccentricity Vector
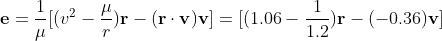
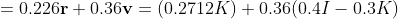
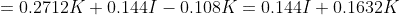
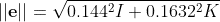
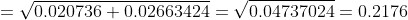
This doesn't match with the textbook answer that e = 0.820748, I've done this question over and over many times and have never arrived at that answer. I'm looking mainly for hints at what might be going wrong here. Thanks for the help!
Finding specific angular momentum
Finding the orbital parameter
Finding Eccentricity Vector
This doesn't match with the textbook answer that e = 0.820748, I've done this question over and over many times and have never arrived at that answer. I'm looking mainly for hints at what might be going wrong here. Thanks for the help!