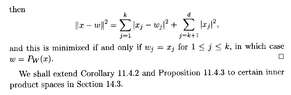Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...
I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...
I need some help to fully understand the proof of Corollary 11.4.3 ...Garling's statement and proof of Corollary 11.4.3 reads as follows:
View attachment 8975
View attachment 8976
In the last sentence of the proof Garling asserts that if $$w_j = x_j$$ for $$1 \leq j \leq k$$ then we have $$w = P_W(x)$$ ...
I cannot formulate an explicit formal and rigorous proof of this statement ... can someone please help me with this ...Help will be appreciated ...
Peter
I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...
I need some help to fully understand the proof of Corollary 11.4.3 ...Garling's statement and proof of Corollary 11.4.3 reads as follows:
View attachment 8975
View attachment 8976
In the last sentence of the proof Garling asserts that if $$w_j = x_j$$ for $$1 \leq j \leq k$$ then we have $$w = P_W(x)$$ ...
I cannot formulate an explicit formal and rigorous proof of this statement ... can someone please help me with this ...Help will be appreciated ...
Peter