ethex
- 25
- 0
Homework Statement
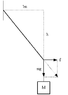
A cable of length L is supported at different elevations and is used to suspend two masses m1=10kg and m2=25kg at B and C respectively, as shown in Fig 2. The vertical heights of B and C relative to the support at A are denoted by h1 and h2 respectively. For simplicity, use g=10m/s^2. Obtain two independent equations relating h1 and h2 and then use them to determine the cable length L if it is desired that h1=h2. If the cable length L=5m, computer h1, h2 and the maximum tension in the cable.
I believe this question is about parabolic cable.
Can give me hints how to start this question? Do i have to make an imaginary cut at part of cable?