giladsof
- 13
- 0
Homework Statement
Homework Equations
U = 0.5CV^2
The Attempt at a Solution
I'm really lost on this one...?
giladsof said:Homework Statement
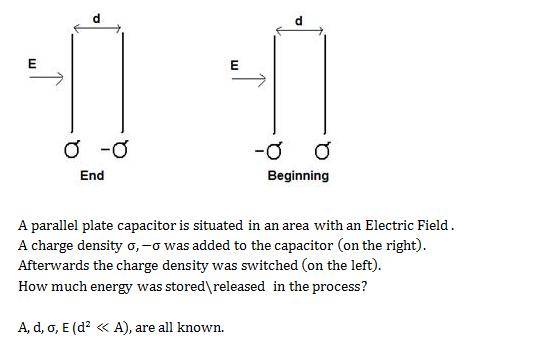
Homework Equations
U = 0.5CV^2
The Attempt at a Solution
I'm really lost on this one...?
zhermes said:Yes, you do seem to be fairly lost on this one.
Is that the only question you had?
giladsof said:Thank you I solved it.
One small question remains- I don't understand why is it so intuitive that the capacitor will resist this change?