Parallel RLC circuit initial values

[ViolentCorpse]

Homework Statement

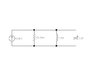
For the circuit shown (in the attachment), find iL(0+) and Vc(0+).

Homework Equations

V=IR

The Attempt at a Solution

At t=0-; the inductor can be replaced by a short-circuit and the capacitor by an open circuit. This shorts out the resistor so by Ohm's law, the voltage drop across it is 0V. Since all the elements are in a parallel combination, that means the voltage across each element is 0V. And we know that Vc(0-)=Vc(0+); therefore Vc(0+)=0V.

For iL, since the inductor acts like a short circuit and at t=0-, all the current passes through this short alone. So iL(0-)=iL(0+)= 4A.

Right?

Now here's my question: An open-circuit equivalent of capacitor means that the capacitor is charged and thus has a voltage across it. Yet in this problem, my analysis yields Vc(0)=0V. I find this result contradictory to my solution approach because I started by open-circuiting the capacitor only to later arrive at the result that it has developed no voltage at all across it; for how can a charged capacitor not have any voltage across its plates?

This is my conceptual confusion. I'd really appreciate your help guys! :)

 

[gneill]

Now here's my question: An open-circuit equivalent of capacitor means that the capacitor is charged and thus has a voltage across it. Yet in this problem, my analysis yields Vc(0)=0V. I find this result contradictory to my solution approach because I started by open-circuiting the capacitor only to later arrive at the result that it has developed no voltage at all across it; for how can a charged capacitor not have any voltage across its plates?

There's no problem or contradiction; zero volts is a perfectly good value for potential.

The reason we consider the capacitor to be an open circuit at steady state is that it has attained whatever potential is required such that further changes cease; it reaches electrical potential equilibrium with its connection points. This value may very well be zero volts if that's what the external circuit demands.

 

[ViolentCorpse]

There's no problem or contradiction; zero volts is a perfectly good value for potential.

The reason we consider the capacitor to be an open circuit at steady state is that it has attained whatever potential is required such that further changes cease; it reaches electrical potential equilibrium with its connection points. This value may very well be zero volts if that's what the external circuit demands.

Ah, I see. Will it be correct to say that in this circuit, the capacitor hasn't been charged at all until t=0 and only the inductor has been charged?

Also, how would this problem change if the current source is replaced by a voltage source of say 4 Volts. All the elements should be getting the same voltage across their terminals i.e 4V, but applying ohm's law on the resistor would suggest otherwise...

Thank you so much, gneill!

 

[gneill]

Ah, I see. Will it be correct to say that in this circuit, the capacitor hasn't been charged at all until t=0 and only the inductor has been charged?

It depends upon how far back in time you wish to look; at some point the circuit must have been assembled and the current source switched on for the first time. In the first instant the inductor will look like an open circuit and the capacitor will begin to charge... some interactions will occur before the circuit eventually settles into a steady state (this is the transient response).

Thank you so much, gneill!

You're quite welcome

 

[ViolentCorpse]

I understand. :)

I've edited my last post. Please take a look at it and bear with me just a little more.

 

[gneill]

Also, how would this problem change if the current source is replaced by a voltage source of say 4 Volts. All the elements should be getting the same voltage across their terminals i.e 4V, but applying ohm's law on the resistor would suggest otherwise...

First tell us what your thoughts are on this. In particular, how would the inductor current behave in such a situation?

 

[ViolentCorpse]

I think it won't be much different from before. The inductor would assume its short-circuit characteristics at steady-state, so all the current (a fairly large current) would be diverted through the inductor.

 

[gneill]

I think it won't be much different from before. The inductor would assume its short-circuit characteristics at steady-state, so all the current (a fairly large current) would be diverted through the inductor.

How large is "fairly large"? Is this a realistic circuit?

 

[ViolentCorpse]

How large is "fairly large"? Is this a realistic circuit?

Umm... I can't give an exact number. Practically, the current would only be impeded by the small wiring and inductor resistances, so it could be dangerously large. I don't think it is a realistic circuit. It may damage the voltage source and the elements involved.

Am I on the right track here?

I think I'm slowly realizing that I asked quite a silly question.

 

[gneill]

Umm... I can't give an exact number. Practically, the current would only be impeded by the small wiring and inductor resistances, so it could be dangerously large. I don't think it is a realistic circuit. It may damage the voltage source and the elements involved.

Am I on the right track here?

I think I'm slowly realizing that I asked quite a silly question.

There are no silly questions

If the components are ideal (zero resistance for all non-resistor components), the inductor current would run away to infinity. So, not a realistic circuit.

However, can you think of how you might change the circuit slightly to make it practical? Hint: you want to prevent the voltage source from ever seeing a short circuit.

 

[ViolentCorpse]

I'm really grateful to you for your continuing kind response, gneill. :)

Hmm, to make the circuit practical... I think the resistor should be put in series with the inductor.

 

[gneill]

I'm really grateful to you for your continuing kind response, gneill. :)

Hmm, to make the circuit practical... I think the resistor should be put in series with the inductor.

Yes, that would work. But even better, put it in series with the voltage source. Then, for the right choice of voltage, the circuit will behave exactly like the one with the current source with the resistor in parallel.

 

[ViolentCorpse]

Thanks a ton, gneill! I really really appreciate your help! :)