Engineering Parameters of transformers: open and short-circuit tests

[Granger]

Homework Statement

Ok I have the following circuit and data (when the subscript is "ef" it means "rms" values):

I am asked to determine the parameters of the transformer r1 L11, L22 and LM with the given experimental data.

Homework Equations

3. The Attempt at a Solution [/B]

I had no problem extracting data from the open circuit experiment.
Using the fact that the active power is given by
$$P=r_1 I_{rms}^2$$

I found $$r_1=10 \Omega$$

Then applying induction law in both primary and secondary leaves us with:

$$u_1(t)=r_1i_1(t)+L_{11}\frac{di_1(t)}{dt}$$
$$u_2(t)=-L_{M}\frac{di_1(t)}{dt}$$

Applying phasor notation and taking the rms values will lead us to obtain

$$L_M=\frac{U_{2_{rms}}}{\omega I_{1_{rms}} }=31.83 mH$$
$$L_{11}=\sqrt{(\frac{U_{1_{rms}}^2}{I_{1_{rms}}^2} - r_1^2) \frac{1}{\omega^2}}=55.13 mH$$

Ok and there is no more data we can extract form the open-circuit experiment.

Passing to the short-circuit experiment I will obtain from induction law again:

$$0=-L_{M}\frac{di_1(t)}{dt}-L_{22}\frac{di_2(t)}{dt}$$

Which leads to

$$L_{22}=\frac{L_M I_{1_{rms}}}{I_{2_{rms}} }$$

Problem now is I don't know the value of the root-mean square of current 2 and have no idea how to find it out.
My guess is that I need to use the reactive power. But how?
I know from Poynting complex theorem:

$$P_Q= 2\omega ((W_e)_{av} - (W_m)_{av})$$

But, and that is another question I have and would like to get ans answer on?
How should I apply this formula.
For the electrical energy, should I take the capacitor? But what's the voltage value? The same as the open-circuit experiment?
And for the magnetic energy? What inductances should I consider? Do I need to calculate an equivalent circuit?

I'm really confused and would appreciate some help. Thanks!

 

[Granger]

Can someone help me please? :(

 

[magoo]

The open circuit test tells you the turns ratio because it gives you the two voltages.

In the short circuit test, you have one of the currents so you should be able to determine the other one given the turns ratio.

 

[Granger]

Thanks for your contribution but that is wrong :/ It makes me obtain a wrong value for L22

 

[gneill]

Thanks for your contribution but that is wrong :/ It makes me obtain a wrong value for L22

Why, what value do you get (show us the calculation please) and what value do you expect to get?

 

[Granger]

I expected to get 27,6 mH
By doing what you guys said I get to a turns ratio of 2 (dividing the voltages voltages). That means the current I2rms is 2 times current I1rms equals to 10V. That means L22 = LM/2 = 15.9 mH

 

[Granger]

@gneill can you help me? please?

 

[gneill]

Hello Granger,

Sorry to have been absent for so long.

I've been taking a look at the problem and have to admit that at this juncture I don't see a way forward. We don't know the coupling constant $k$ between the loops ($L_M = k\sqrt{L_{11}L_{22}}$) nor do we know anything else about the secondary loop except for the induced voltage for a given primary current ($i_1 j \omega L_M$). The $P_{var}$ gives us part of the primary current, but I don't think that we can find the real portion of the primary current without knowing how the source represented by the mutual inductance (and controlled by the secondary) will affect the primary.

At first I thought that we could derive the real part of the primary current given that the magnitude of the apparent power should be (100 V)(5 A) which assumes that $U_1$ is providing all the power to the transformer part of the circuit, but this turned out to be a false lead since again, the influence of the secondary on the primary contributes to the current in the primary.

You said that you were expecting a value of $26.7\; mH$ for the secondary inductor. Is this a provided solution value?

Anyway, as I said, I personally don't see a way forward with this problem. I would be keen to know if you or others find a way.

Please let me know if you find a solution. I'll also watch this thread to see if other (perhaps more brainy than me) members have a clever idea.

 

[jim hardy]

I'm not familiar with that term P_q which they tell us is 144.3 Var.

What do we know about this? People who write homework questions usually include some subtlety to encourage us to reason, or as i say "grunt it out"...
So let's think of it as just a less than ideal transformer with nonzero leakage reactances and nonzero primary resistance (i see secondary resistance was defined zero)

If i assume that P_q is the imaginary component of primary VA in short circuit test
and more significantly that r₂ = 0
Then i know that secondary current is all reactive
Curiously , primary current didn't change its magnitude when secondary became short circuited, only its phase
I think i'd calculate what was primary reactive current for both tests
because the change in it is all due to secondary amp-turns cancelling primary amp-turns in L_M.

CAVEAT i haven't yet attempted to put numbers to that approach ,
just that's how i solve word problems - keep poking at them until something makes sense.

I might be able look further this evening... got to make use of the daylight his afternoon.

meantime i hope above helps -
and i hope it's not resonant at 50 hz ...

old jim
.

 

[gneill]

Curiously , primary current didn't change its magnitude when secondary became short circuited, only its phase

I suspect that they've changed the driving voltage to achieve a 5 A (rms) current in the primary. Note that they don't specify U_1ef for the short circuit test.

 

[magoo]

If his P_q is 144.3 vars, then I^2 X_L11 equals that. So, I get 5.772 ohms inductive reactance.

Knowing that I1 = 5, we can determine the voltage for the short circuit test. I get 28.86 V which is lower than the 100 V used in the open circuit test - as qneill suggested.

 

[gneill]

If his P_q is 144.3 vars, then I^2 X_L11 equals that. So, I get 5.772 ohms inductive reactance.

The mutual inductance is going to have an influence. The current in the secondary will feed back to the primary in the amount $i_2 j \omega L_M$ Volts. So $L_M$ and $i_2$ need to be taken into account. We might get an idea of what $i_2$ is from the coupling ratio implied from the open-circuit test, given that the secondary resistance is given to be approximately zero. There the emf across the primary inductance is not $U_1$, but rather $U_1 - Ir_1$, where $I$ is the 5 A specified.

 

[jim hardy]

Let us for the moment ignore the capacitor and any effects of resonance .
I'll work it using old fashioned AC circuit analysis , not challenging your approach but building confidence in my own arithmetic.

Open Circuit Test
5 amps X Z_{of transformer} = 100 volts
so Z = 20 ohms = R+jX_L11 , and R = 10 ohms (obviously)
and Pythagoras tells us that's a 1::2::√3 , or 30/60/90 degree right triangle
20 = 10+j√300
X_L11 √300 (= 17.32) ohms which at 50 hz = 55.13 millHenries ,same as you got.
and Z = 20 at angle ∠60°
so I = V/Z = 100∠0 / 20∠60 = 5∠-60° =2.5 -j4.33 amps
EDIT
Short Circuit Test isn't working out for me. I believe the capacitor current is included in the Pq term which isn't evident from the drawing provided.
So I'm deleting the remainder of this post and a couple false start posts that followed.

 

[jim hardy]

Another false start deleted. old jim

 

[jim hardy]

i thought it was insoluble as given. I got quadratics to solve which are implausible for a textbook problem.
and after further reading my mistake became apparent.
What i ascribed to leakage inductance was instead due to turns ratio.
Looking into the mutual inductance method of handling turns ratio
a solution looks pretty straightforward
i was pretty well along but Latex has beat me into submission.You can't copyand paste it. i am defeated for now
not by algebra but by Latex

approach is
calculate Xprimary from OC test it's √300 ohms so Lprimary = $\frac{√300}{100π}H = 55.13mH$
calculate Xmutual from OC test (it's 10 ohms) so Lm = $\frac{10}{100π} = 31.83 mH$
Hyperphysics tells us how mutual inductance relates primary to secondary inductance

Knowing Lmutual and Lprimary allows us to calculate Lsecondaryfrom before i tried to paste Latex

and even there I'm missing the √ radical in numerator of Lprimary... but i can't make Latex write the expression
$Lsecondary = \sqrt {\frac {Lmutual ^2} {Lprimary}}$
where my L's are fractions themselves .

Anyhow

knowing L_secondary we can find I_secondary -
it's 50 volts/_XLsecondary

So new we know every term in these two equations

and it ought to be solved with ease.
i might try some more Latex tonight , but right now I'm in more this kind of mood

 

[jim hardy]

okay, on to short circuit test...

$Lsecondary = \frac{Lmutual^2} {Lprimary}$
$Lsecondary = \left( \frac{10}{100π}\right)^2$ divided by $\frac{\sqrt{300}}{100π} = \frac{10}{100π} X \frac{10}{100π} X \frac{100π}{\sqrt{300}} = \frac {1}{π\sqrt{300}} = 18.377 mH$
and at 50 hz (ω= 100π), ωLsecondary is $\frac{100π}{π\sqrt{300}} = \frac{100}{\sqrt{300}} = 5.7735 ohms$

and $Isecondary = \frac{50v} {jωLsecondary}$ $= \frac {50} {\frac {100}{√300}} = \frac{\sqrt{300}}{2} = 5\sqrt{3} = 8.6602 amps$
How about that it's a transformer !
$\frac{Ip}{Is} = \frac{Vs}{Vp}$
I should have believed in my basics.

Okay, so secondary amp-turns cancel primary amp turns reducing counter-EMF.in Lprimary
In the amount of $Isecondary$ X $Xmutual$
Xmutual was determined 10 ohms from OC test

so at 5 amps in the SC test we find this term

5√3 amps X 10 ohms = 50√3 = 86.6 volts
which exactly equals the counter-emf in Lprimary
Xprimary was found in OC test equal to $\sqrt{300}$ ohms, which X 5 amps is 86.6 volts.
so they exactly cancel leaving the shorted transformer a purely resistive circuit ,
that is Pq = 0 VArs.

That means Vapplied must be 50 volts.

EDIT i finally figured out how to solve it , so am striking this statement: So i challenge the statement

One might posit coupling less than 1 (presence of leakage reactance )
that's how i started , and the algebra got so cumbersome i decided it was not likely that's what the author intended to teach with this problem.
EDIT it worled out after all. Just my restiness.

Was this one solved in class ? I'd sure like to know if i should have continued on a "less than perfect coupling" tack instead
EDIT that worked.see posts 18 and 21

 

[jim hardy]

here is a pretty good tutorial
https://www.rose-hulman.edu/class/ee/HTML/ECE370/PDFs/Review of Ideal Transformers.pdf

it shows how to handle leakage flux by adjusting the relation between mutual and winding inductances .

k = 1 - (fraction of flux that leaks).

 

[jim hardy]

wow I've procrastinated for two weeks ?
Dread of Latex .

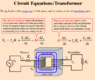
using the tool of Mutual Inductance

where k is the fraction of flux that couples both coils, ie doesn't leak.
k of 1 is 'ideal coupling'
L2 then = $\frac{M^2}{k^2L1}$

we redraw the circuit showing the interaction between windings as dependent voltage sources
in the primary is a dependent voltage source , with polarity aiding the applied voltage, with amplitude jωI₂M
and
in the secondary is a dependent voltage source, with polarity to satisfy the dot convention, and of amplitude jωI₁M .
as drawn above.
So they criss-cross. Primary current sets secondary OC voltage, and secondary current reduces primary counter-emf.
Mutual inductance M takes care of the turns ratios and k handles leakage flux.Ignoring the capacitor that was in the original image
we have found from open circuit test,
where I1 was 5 amps, primary volts 100 and secondary voltage 50 ,
r₁ = $\frac{250}{I_1^2} = 10 Ω$
jωL₁ = √300 ohms , so L₁ = $\frac{\sqrt{300}}{100π}$ = 0.05513 Henry

Ohms of Mutual Inductance jwL_M = 50V/5 amps = 10 ohms, so M =10/100π = $\frac{1}{10π}$ = 0.03183 Henry

.........

From short circuit test
we learn that at 5 amps of primary current
P_q = 144.3 var
and since the only resistance present is the ten ohms of r₁, power must still be 250 Watts
giving total VA of $\sqrt{250^2 + 144.3^2} = 288.65...$ VA
which dictates an impedance angle of 29.99354 degrees -
(for a textbook problem that's sooo diggone close to 30 that i have to think it's result of truncation
but i'll work with his numbers as given , however i will round to 4 digits)

288.65 VA at 5 amps dictates 57.73 volts
144.3 vars at 5 amps dictates 28.86 volts across the inductance, and that divided by 5 amps = 5.772 ohms
250 watts at 5 amps dictates 50 volts across the resistance
and sure enough, that makes a right triangle because √(50² + 28.86²) = 57.73...
so I'm confident enough to continue

Writing KVL around primary

we find
$V1 = I1R1 + jωI1L1 -jw MI2$ and we'll call that EQ(1)
and
and L2 = $\frac{M^2}{k^2L1}$
Now
$I2 = Vsec / L2$ EDIT make that $I2 = Vsec / jωL2$ and i forgot more jω's so added them in following lines , and i tried but latex won't let me make them red
and $Vsec = jω MI1$
so $I2 = jωMI1 X \frac{k^2L1}{M^2}$
and voltage source jωMI2 has amplitude $\frac{jωM⋅M⋅ I1⋅k^2L1}{M^2}$ = $jω k^2I1L1$, M's cancel fortunately

substituting that for last term of EQ(1)
$V1 = I1R1 + jωI1L1 -jw k^2I1L1$
$V1 = I1 X (R1 +jωL1 - k^2L1)$
$\frac{V1}{I1} = R1 + jωL1 (1-k^2)$

AHA ! We know the right half of that equation is the impedance
looking at the reactance term
we know jωL1 is $\sqrt{300} Ω$ from OC test, and that's 17.32
and from SC test $jωL1 (1-k^2) = 5.772 Ω$
so
$jωL1(1-k^2) = 5.772$
divided by
$jωL1 = 17.32$
yields
$1-k^2 = \frac{5.772}{17.32} = 0.3332$
$k^2 = 0.6667$
$k = 0.8165$

$L2 = \frac{M^2}{k^2L1}$
$L2 = \frac{ 0,03183 ^2 }{0.6667 X 0.05513 } = 0.02756 Henry$
$jωL2 = 0.02756 X 100π = 8.658 Ω$
$I2 = \frac{jwMI1}{jωL2} = \frac{50}{8.658} = 5.775 amps$

gotta be a silly arithmetic mistake in there someplace
as you guys know I'm a plodder
but i think that algorithm is viable

i'd like to go back and work it with a couple more digits in author's Pq vars
Had he given us 144.33756267.. vars for Pq, just 0,0375 more ,, he'd have hit 30 degrees exactly. That's why i think it got truncated.
We'd then have 288.67 VA (500/√3) and a 30-60-90 triangle
and he'd have shifted from 60-30-90 to 60 30-60-90 impedance triangles by shorting the secondary, which sounds like something i'd do if tinkering with trig .
that way it'd have nice even 1-2-√3 Pythagorean related arguments for all those impedances, voltages and currents which would just seem elegant.

but 'm Latex-ed out for now.
and @@**()*&^&^%$ latex just quit showing in preview so i hope the jw's are right now

find my mistakes ?old jim

 

[jim hardy]

from a Nov 28, post #6

I expected to get 27,6 mH

will 27.56 do ?

 

[Tom.G]

@jim hardy Seems to prove your post #18 conjecture of truncation errors.

 

[jim hardy]

conjecture of truncation errors.

If the angle were exactly 30 degrees, ie Pq were 500/√3 sin(30) = 250/√3 = 144.337_etcetera

then volts across reactance (1-k^2)jωL1 would be $\frac{Pq}{I1} = \frac{\frac{250}{√3} volt-amps}{5 amps} = \frac{50}{√3} volts$
and (1-k^2)jwL1 would be $\frac{volts~across~it}{amps~through~it } = \frac{10}{√3} Ω$
and (1-k^2)L1 would be $\frac{10}{ω√3} = \frac{10}{100π√3} = \frac{1}{10π√3}$ Henry

jω(1-k^2)L1 = 10/√3
and
jωL1 = √300 from OC test
dividing those two yields
(1-k² ) = (10/√3) /√300 = 10/30 = 1/3
k^2 = 2/3
k = √(2/3)

L2 = M²/k²L1
M = 10/100π = 1/10π
M² = 1/100π²
k² - 2/3
L1 = (√300) / (100π)

so $L2 = \frac{M^2}{k^2} X \frac{1}{L1}$
$L2 = \frac{ \frac{1}{100π^2}}{\frac{2}{3}} X \frac{100π}{√300}$

$L2 = \frac{3}{200π^2} X \frac{100π}{\sqrt{300}}$$L2 = \frac{3}{2π\sqrt{300}} = 0.027566...$ , 27.567milihenry

and k = √(2/3) = 0.8164_etcetera
so leakage = 1-√(2/3) = 0.1835_etcetera

i sure like a problem with numbers all related like that where you don't lose any digits from rounding along the way. I wonder if that was author's intent.