Chantry09
- 59
- 0
Im having a hard time getting my head around this, any help would be much appreciated.
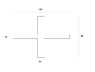
Determine the position of the centroid and calculate the second moment of area about a horizontal axis passing through the centroid for the following sections shown. Attached is the image of the shape, including dimensions.
A x Y(bar) = (A1 x Y1) + (A2 x Y2)
IX = Ix + Ah(squared) [Not sure if this equation is correct]
I know Y(bar) to equal 40mm for the attached shape. However i don't know how to get from the y(bar) to the position of the centriod. The answer should be 862000.0mm, i just don't know how to get there, everything i try comes up with a different result.
Homework Statement
Determine the position of the centroid and calculate the second moment of area about a horizontal axis passing through the centroid for the following sections shown. Attached is the image of the shape, including dimensions.
Homework Equations
A x Y(bar) = (A1 x Y1) + (A2 x Y2)
IX = Ix + Ah(squared) [Not sure if this equation is correct]
The Attempt at a Solution
I know Y(bar) to equal 40mm for the attached shape. However i don't know how to get from the y(bar) to the position of the centriod. The answer should be 862000.0mm, i just don't know how to get there, everything i try comes up with a different result.