Terrycho
- 20
- 2
- Homework Statement
- Consider the following linear first-order PDE
- Relevant Equations
- Partial Differential Equations
Consider the following linear first-order PDE,
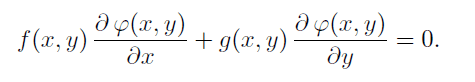
Find the solution φ(x,y) by choosing a suitable boundary condition for the case f(x,y)=y and g(x,y)=x.
---------------------------------------------------------------------------
The equation above is the PDE I have to solve and I denoted the following result by solving it.
φ(x,y)=F(t)=F(1/2 x^2 - 1/2 y^2)
So, I set the boundary condition as φ(2y, -y)=3y^2 and denoted the following result.
φ(x,y)=x^2 - y^2.
Here is my question. While I was solving the equation, I got F(t)=2t, where t=(3y^2)/2, but how do I know if this F(t) meets all the characteristic curves? Here, the characteristic curves are determined by t= x^2/2 - y^2/2 for each constant t.
Find the solution φ(x,y) by choosing a suitable boundary condition for the case f(x,y)=y and g(x,y)=x.
---------------------------------------------------------------------------
The equation above is the PDE I have to solve and I denoted the following result by solving it.
φ(x,y)=F(t)=F(1/2 x^2 - 1/2 y^2)
So, I set the boundary condition as φ(2y, -y)=3y^2 and denoted the following result.
φ(x,y)=x^2 - y^2.
Here is my question. While I was solving the equation, I got F(t)=2t, where t=(3y^2)/2, but how do I know if this F(t) meets all the characteristic curves? Here, the characteristic curves are determined by t= x^2/2 - y^2/2 for each constant t.
Last edited: