Particle motion in non-uniform electric field

[mitleid]

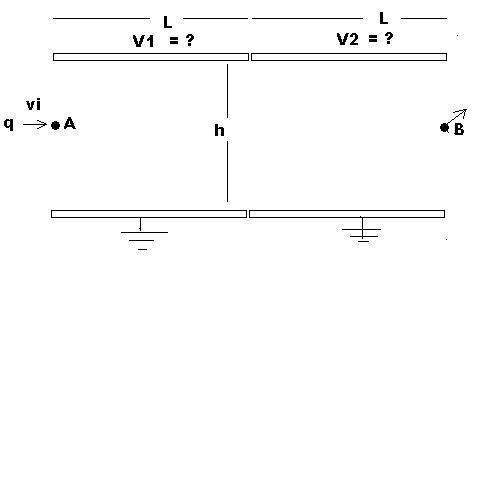
Two adjacent parallel plate capacitors are used to deflect charged particles as shown in the figure. The relevant dimensions l and h are shown. The lower capacitor plates are grounded while the upper plates are kept at some voltages V1 and V2, which are to be found in this problem given the following.

A positively charged particle q with mass m enters horizontally at point A. After executing some trajectory, the particle exits at point B, which has the same vertical position as point A. However, the velocity at B is not horizontal, and has some component Vy. What are the potentials? Neglect the effects of gravity.

Some relevant equations :
F = qE
Acceleration (a) = F / m = qE/m

mechanics:
x = Vi*t
y = - (qE/2m)t^2
Vfx = Vi
Vfy = -(qE/m)*(1/Vi)

I think I have most of what I need here. This next figure illustrates how I think the two trajectories take place, and I wanted to check this before I went further.

Since the bottom plates are grounded, voltage across them is equal to 0. E points from higher to lower potentials, so the field would expected to be downwards.

A downward field would correspond to the first hypothetical trajectory. However, for Vy to be "positive" or upwards, an upward field would have to take place for the second trajectory. Thus V = 0 would have to be higher than V2, making it negative or also equal to 0.

Am I headed in the right direction?

 

[learningphysics]

x = Vi*t
y = - (qE/2m)t^2
Vfx = Vi
Vfy = -(qE/m)*(L/Vi)

That's what you meant right?

Looks good to me.

xf = L
yf = (-qE/2m)(L/Vi)^2
Vfx = Vi
Vfy = -(qE/m)*(L/Vi)

so that's after the first stage...

what do you get after the second stage...

the curve should be smooth... you have an abrupt change... instead the trajectory is a smooth curve that goes downwards reaches a minimum then goes back upwards.

 

[mitleid]

There we go.

Since it enters and exits at the same height, and the distance along each plate is the same (L), $$\Delta$$y MUST be the same for each side, but opposite polarity. It could go up and then down (and have a negative y component velocity), or down and then up, which applies here.

Hence |V1| = |V2|.

Additionally, Va - Vb = E*h, where Va is the voltage on the top plate, and Vb is the bottom. Vb = 0 since it is grounded, so V1 = E * h

Solving for E from the above equation for Vfy :

E1 = - Vfy (m/q) (Vi/2L)

I multiply this by h to get V1, which is equal in magnitude to V2.

However... the direction of E is different for each plate. Do I need to solve for each field...? I would have to start making up variables for the state of the particle @ distance L, to get the initial velocity for the motion through the second plates. Maybe I should just keep my first answer...

 

[learningphysics]

I don't think |V1| equals |V2| ...

continue to solve through kinemtics as you were doing... call the field in the first stage E1... the field in the second stage E2... you can get the voltages afterwards using V = Eh...

the object enters the second field at an angle downwards... keeps going down as it enters the second field... gets to some minimum value and goes back up.

but all that doesn't matter... just let the equations take care of that...

 

[mitleid]

So more like this...

All right. So I will separate into initial stage, stage 1 (after traveling distance L) and stage 2 (after traveling distance 2L).

I need to know$$\Delta$$y at stage 1, but to get this I also need E1.

v1y = - (qE1/2m)(L/vi)

E1 = - v1y (2m/q)(vi/L)

v1x = vi

Hmm. i guess since this is a trajectory, when vy is a minimum it will be equal to zero. not sure if that helps me at this point though...

 

[learningphysics]

xf = L
yf = (-qE1/2m)(L/Vi)^2
Vfx = Vi
Vfy = -(qE1/m)*(L/Vi)

the above is after the first stage...

so now we have E2 in the second stage acting upward...

y = y0 + vy*t + (1/2)at^2

y = (-qE1/2m)(L/Vi)^2 - (qE1/m)*(L/Vi)*t + (1/2)qE2/m*t^2

measuring t from the moment it enters the second stage...

it reaches the end of the second stage at t = L/Vi... it has to get back to y=0.

plug in t = L/Vi and y = 0, into:

y = (-qE1/2m)(L/Vi)^2 -(qE1/m)*(L/Vi)*t + (1/2)qE2/m*t^2

that gives a relationship between E1 and E2. Solve for E2 in terms of E1.

finally use

v_ver = v0y + (qE2/m)*t

when it exits the second stage it has a vertical component Vy (I think this is what the question says... it exits with some "component" Vy... does that mean vertical component?)

so:

Vy = -(qE1/m)*(L/Vi) + (qE2/m)*(L/Vi)

plug in E2 in terms of E1... then solve for E1 (which will be in terms of L, Vi, Vy, and m)

Then you can get E2...

V1 = hE1. V2 = -hE2.