Path Integral - Cartesian to Polar Coordinates

[SeanGillespie]

Homework Statement

Transform to polar coordinates and evaluate...

\int^{a/\sqrt{2}}_{0} dx\int^{\sqrt{a^2-x^2}}_{x}\sqrt{x^2 + y^2}dy

Homework Equations

x^2 + y^2 = r^2
x = r cos \theta
y = r sin \theta

I've been struggling to make sense of this problem, it should be easy, I'm just not arriving at the correct answer. I'm struggling to understand how to change the limits to the polar coordinate limits, and I also don't understand where the function sqrt{x^2 + y^2} 'disappears' to.

I do understand that the dxdy becomes rdrd(theta) however.

Some guidelines on converting the limits and a little explanation would be very much appreciated.

Edit:
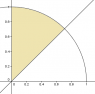
To expand on my post, I have sketched out the previous limits of the integral, and it is clear that the integral is over a 45 degree segment of a circle. However rather than graph sketching I would be interested to know if there is an analytical way of arriving at the new limits.

I'm still clueless about where the abovementioned square-root "disappears" to, my assumption was that I could substitute it for r (which also appears to be constant 'a'), however by doing so and evaluating the integral I obtain the wrong answer.

 

[hunt_mat]

So what you have is the integral:
<br /> \int_{0}^{a^{2}/\sqrt{2}}\int_{x}^{\sqrt{a^{2}-x^{2}}}\sqrt{x^{2}+y^{2}}dxdy<br />
First things first, draw a picture of the region of integration. The a and r are different so your \sqrt{x^{2}+y^{2}}=r

 

[SeanGillespie]

I've sketched the region of integration, and it is clear what the new limits should be. However, as you said, by substituting the sqrt for r and evaluating the integral I obtain an answer of:
a^3\pi/12

The answer expected is:
a^2\pi/8

Either the question is wrong, or I'm wrong, I assumed I was wrong, hence why I felt I might be misunderstanding the problem. The answer given is obtained if you pretend the square-root isn't even there... I figured it might be cancelling out somehow, but if it is then it's beyond my understanding how it does so.

Any idea?

 

[hunt_mat]

Can you go through your workings so I can see what is going on please.

 

[SeanGillespie]

Original integral:
\int^{a/\sqrt{2}}_{0}dx\int^{\sqrt{a^2-x^2}}_{x}\sqrt{x^2+y^2}dy

Replace dxdy with r dr d(theta) and change the limits:
\int^{\pi/2}_{\pi/4}d\theta\int^{a}_{0}\sqrt{x^2+y^2} r dr

By replacing the square root with r, I then have:
\int^{\pi/2}_{\pi/4}d\theta\int^{a}_{0} r^2 dr

By evaluating that I get:
a^3\pi/12
Which is supposedly the wrong answer.

The answer my tutor has given me is obtained from the integral:
\int^{\pi/2}_{\pi/4}d\theta\int^{a}_{0} r dr

Which is where I'm confused, what happened to the extra r?

 

[hunt_mat]

First of all, what is the region of integration

 

[SeanGillespie]

see attached image.

The shaded region is the region of integration. For the sake of making it easier to draw I've taken a to be 1. 'a' will simply be where the curve:
y = \sqrt{a^2 - x^2}
crosses the axes, as it is also the radius of the circle.

So for the y part of the integral, the integral is evaluated to obtain the height of the strips between the line y=x and the curve (shown above). The x part then sums these strips, so is its limits are therefore between x=0 and x=a/sqrt(2), the upper limit being the point at which the curve and line, y=x intersect.

It is clear that by converting this into polar coordinates the limits become:
r = 0\ to\ r = a
and
\theta = \pi/4\ to\ \theta = \pi/2

Is this not correct?

 

[hunt_mat]

It looks good to me, I did the integral and I got the same answer as you did. I am just checking the answer with mathematica. You could do the integral straight off of course as a check for the polar co-ordinates.

 

[SeanGillespie]

I'll take it that the answer I was given on the problem sheet is wrong then, and that my method of calculating it is correct. Thank you very much.

 

[hunt_mat]

You're welcome