milk242
- 2
- 0
Pendulum measuring the restorative force HELP!
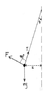
A pendulum with length L is suspended at an angle theta. At the bottom of the pendulum, a string is attached to force meter. The string attached to the force meter is perpendicular to the pendulum string. In terms of F and theta, find an expression for mass.
Fg= -mg
(Fg)r = -mgcos(theta)
(Fg)t = -mgsin(theta)
What I get is all the tangential and radial components cancel out equally zero, which I would expect because mass doesn't matter in a pendulum. So I don't understand how I'm suppose to obtain an expression for mass.
Homework Statement
A pendulum with length L is suspended at an angle theta. At the bottom of the pendulum, a string is attached to force meter. The string attached to the force meter is perpendicular to the pendulum string. In terms of F and theta, find an expression for mass.
Homework Equations
Fg= -mg
(Fg)r = -mgcos(theta)
(Fg)t = -mgsin(theta)
The Attempt at a Solution
What I get is all the tangential and radial components cancel out equally zero, which I would expect because mass doesn't matter in a pendulum. So I don't understand how I'm suppose to obtain an expression for mass.