- #1
dkoppes
- 3
- 0
Homework Statement
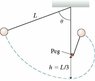
A pendulum is formed from a small ball of mass m on a string of length L. As the figure shows, a peg is height h = L/3 above the pendulum's lowest point.
From what minimum angle must the pendulum be released in order for the ball to go over the top of the peg without the string going slack?
Homework Equations
The Attempt at a Solution
I attempted to calculate the potential energy that the ball starts with at when it is released using PE = (L-L*cos(theta))*m*g and then using the potential energy at the top of the swing around the peg PE = 2/3*L*m*g and then setting them equal to each other find theta. I also tried a couple different methods that we basically just stabs in the dark and these that I just gave are the only ones that make sense. So far I have tried theta = 48.2, 70.5, and 19.5 but it says that all of these are wrong. Please help me.