Penrose diagram of black hole with a changing event horizon

[Sonderval]

Dear all,

I have a question on Penrose diagrams. Consider a collapsing star that forms a black hole with a Schwarzschild radius normalized to 1. What happens in the Penrose diagram when additional matter falls in? I suspect the diagram then has to look like this :

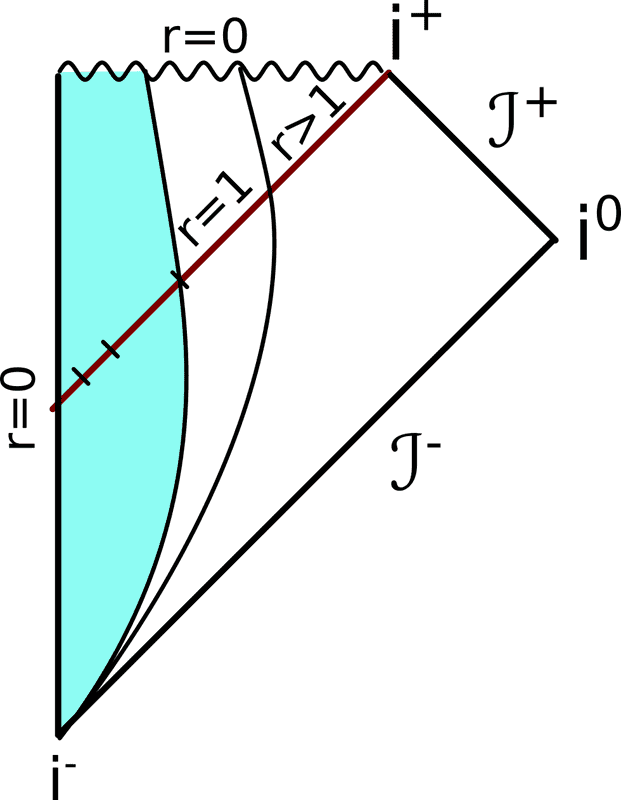
When the outer shell (second curved line) reaches the event horizon, the radius of the BH will increase (r>1). Is this diagram correct? If so, what would happen when a photon is emitted exactly at the moment the BH forms? This photon would then be frozen at the event horizon, but from the diagram it seems as if it could actually move outward to the greater event horizon (because it follows a 45-degree line). Or is this way of thinking incorrect and the diagram looks different?

The second question is related. Here is the diagram for an evaporating BH (from inspirehep)

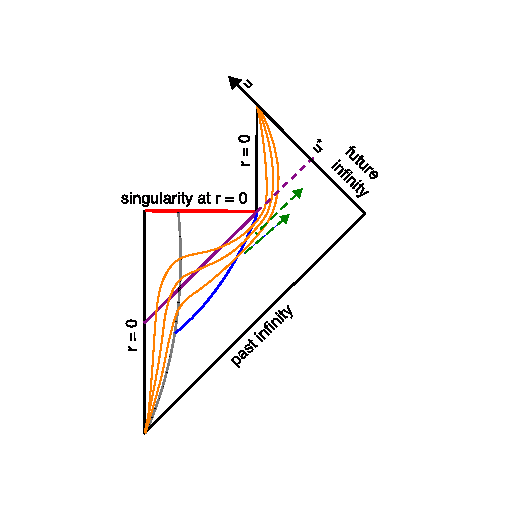
Again, I am wondering what happens to a photon trapped at the event horizon when the hole shrinks? Will it be "sucked inwards" and stay at the event horizon until the BH has evaporated completely and will then emerge from the r=0-position?
Thanks for any help,
Martin

 

[PeterDonis]

What happens in the Penrose diagram when additional matter falls in?

Basically what you describe, yes.

what happens to a photon trapped at the event horizon when the hole shrinks?

It stays at the horizon. That's the definition of the horizon.

Remember that the Penrose diagram is using coordinates that have been specially adjusted to make the horizon be that particular 45 degree up and to the right line, regardless of what happens to the hole. It can gain mass from things falling in, lose mass by evaporation, and even disappear, as your second diagram shows, and none of that changes the horizon line--because the Penrose diagram coordinates are adjusted, using the entire history of the spacetime as input, to make the horizon line look like that.

In other words, the Penrose diagram is not very helpful if you want to understand the dynamics of the spacetime--what things look like locally to a particular observer. The purpose of the Penrose diagram is to easily show certain global properties of the spacetime, which is why it has to use the entire global history of the spacetime for its construction. From a local observer's viewpoint, a Penrose diagram can't even be constructed; the observer would have to know the entire future history of the entire spacetime to know where on a Penrose diagram his particular worldline fits.

 

[Sonderval]

@PeterDonis
Thanks a lot.

It stays at the horizon. That's the definition of the horizon.

I assume the same is true for the case of the expanding hole.
I find this somewhat surprising - the black hole expands and the photon moves "outwards" - but that's probably simply a consequence of using global coordinates. OTOH, it shows that Penrose diagrams are really useful for eactly this kind of consideration.
Thanks again,
Martin.

 

[PeterDonis]

I assume the same is true for the case of the expanding hole.

Yes.