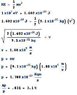dangsy
- 14
- 0
Homework Statement
The position and momentum of a 1KeV electron are simultaneously determined. If its position is located to within 1Angstrom (Δx), what is the PERCENTAGE of uncertainty in its momentum?
Homework Equations
ΔxΔp >= h(bar)/2
The Attempt at a Solution
Δx = 1A = 1x10^-10m
Δp>= h(bar)/2Δx
Δp = 1.055x10^-34(kg/m^2)/s
-------------------------
2(1x10^-10m)
= 5.275x10^-25 kgm/s
how do I get the percentage of uncertainty?