Perfect Ball on Perfectly Frictionless Ramp - Does it Roll or Slide?

[PeterPumpkin]

Homework Statement

Does a perfect ball roll or slide down a perfectly frictionless ramp?

Homework Equations

The Attempt at a Solution

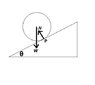
Let P be the contact point of the ball with the ramp.

Then it appears to me there is a torque (about the contact point, P) acting on the ball due to its weight, W. Therefore it should rotate ie roll.

Is this right?


(The torque has magnitude W*R*tan(Theta) where R is the radius of the ball and Theta is the angle of the ramp. The Normal force does not exert a torque as it passes through P. )

 

[Phrak]

Where is the normal force directed through the ball?

 

[PeterPumpkin]

As noted in the original post, the normal force passes through the point of contact, P, and through the center of the ball.

Therefore, there is NO torque due to the normal force about P.

 

[Phrak]

As noted in the original post, the normal force passes through the point of contact, P, and through the center of the ball.

Therefore, there is NO torque due to the normal force about P.

OK. I got to the point where you contrarily noted torque, and stopped reading. So what don't you understand?

It would require torque to change angular velocity. The question implies by omission, but does not state, that it is not rotating to begin with.

 

[PeterPumpkin]

I presume it is not moving to start with.

I was wondering if my original analysis was correct?

 

[Doc Al]

Then it appears to me there is a torque (about the contact point, P) acting on the ball due to its weight, W. Therefore it should rotate ie roll.

Is this right?

It's half right.

It's certainly true that the weight exerts a torque about the contact point, but you cannot conclude from that that the ball will start rolling.

Hint: Consider torques about the ball's center of mass, where a non-zero torque would imply an angular acceleration.

 

[PeterPumpkin]

I have been researching this question elsewhere (see links below). And it seems the ball will SLIDE rather than roll! I don’t understand this! I thought a torque measured the tendency of a body to rotate.

Why doesn’t the torque about the point of contact (P) cause rolling?
Why is friction is needed to cause rolling?
I’m puzzled!

LINKS:
1) I found a thread in Physics Forums > Physics > Classical Physics called
“Can a ball roll down a frictionless plane?” Posted by physics_liker
(https://www.physicsforums.com/showthread.php?t=271692&highlight=friction)

2) I found another thread in “Ask a scientist” (Argonne National Laboratory) called "Sliding Versus Rolling on Friction Free Incline" posted by Alicia
(http://Newton.dep.anl.gov/aasquesv.htm
www.Newton.dep.anl.gov/askasci/phy05/phy05139.htm)

Any other links?

 

[Doc Al]

I have been researching this question elsewhere (see links below). And it seems the ball will SLIDE rather than roll!

That's true, since there's no torque about its center of mass.

I don’t understand this! I thought a torque measured the tendency of a body to rotate.

In many cases it does, but not in all cases. If you measure torques about the center of mass (or about a fixed axis) then you can conclude that a non-zero torque implies an angular acceleration.

Why doesn’t the torque about the point of contact (P) cause rolling?

Because the point of contact is accelerating. Don't use an accelerating point--other than the center of mass--as a reference for calculating torques.

Why is friction is needed to cause rolling?

A force is needed to create a torque about the center of mass. Friction provides that torque.

 

[ideasrule]

But the ball does roll about point P. The ball's center of mass is moving down the slope, which means the line connecting P with the C.O.M. is rotating counterclockwise.

 

[Doc Al]

But the ball does roll about point P. The ball's center of mass is moving down the slope, which means the line connecting P with the C.O.M. is rotating counterclockwise.

No, the point P moves in parallel with the ball's center of mass.

 

[ideasrule]

No, the point P moves in parallel with the ball's center of mass.

Oh, I'm sorry, I thought P was supposed to be a point on the ramp. Now I see that everybody who mentioned it intended it to be on the ball, moving with the ball.

 

[PeterPumpkin]

P is the point of contact with the ball and the ramp. So it is constantly changing if the ball is rolling.

 

[PeterPumpkin]

If what is said is correct, then a wooden cylindrical rod standing on end on a frictionless ramp would NOT topple over (ie rotate)? It would simply slide down the ramp still standing on end!

Does this seem counter-intuitive to you? I thought it would topple over.

 

[ideasrule]

If what is said is correct, then a wooden cylindrical rod standing on end on a frictionless ramp would NOT topple over (ie rotate)? It would simply slide down the ramp still standing on end!

Does this seem counter-intuitive to you? I thought it would topple over.

It does seem counter-intuitive, but we're not used to dealing with frictionless objects. If there's even a tiny bit of friction between the rod and the ramp, the rod would indeed topple over.

 

[PeterPumpkin]

Thanks all. I see I am going to have change my idea about an unbalanced torque implying rolling!