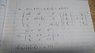Perturbation matrix: free electron model on a square lattice

[Fek]

Homework Statement

Nearly free electron model in a 2D lattice. Consider a divalent 2D metal with a square lattice and one atom per primitive lattice cell. The periodic potential has two Fourier components V10 and V11, corresponding to G = (1,0) and (1,1). Both are negative and mod(V10) > mod(V11).

Write down the secular equation and obtain an expression for the electron energies at k = (pi /a, 0).

Homework Equations

The Attempt at a Solution

Please see attached file (question also attached (part (i). I believe this is wrong but I cannot see what the expectation of the potential between the two final states can be other than zero (as they are separated by a reciprocal lattice vector (0,1).

 

[Fek]

All sorted thank you.