[PhD Qualifier] Liquid in a rotating arm

[confuted]

Homework Statement

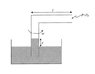
An open glass tube of uniform bore (uniform inner diameter) is bent into the shape of an "L". One arm is immersed into a liquid of density $$\rho$$ and the other arm of length l remains in the air in a horizontal orientation. The tube is rotated with constant angular speed $$\omega$$ about the axis of the vertical arm. Show that the height y to which the liquid rises in the vertical arm is

$$y=\frac{P_0}{g\rho}\left(1-exp\left[-\frac{\omega^2 l^2 M}{2RT}\right]\right)$$​

where $$P_0$$ is the atmospheric pressure and M is the molecular weight of air and R is the universal gas constant. Assume that the air pressure inside open end of the tube is atmospheric pressure, as shown (see attached).

Homework Equations

pV=nRT
$$\rho_{air}=\frac{m}{V}=\frac{MP_0}{RT}$$ (from ideal gas law)

The Attempt at a Solution

I thought about trying to kludge something together with the centripetal acceleration causing a difference in pressure, but that didn't work out for me. Then I looked up Bernoulli's principle, and I don't see how I'm going to get an exponential out of that. What's the appropriate law here?

 

[badphysicist]

I think that I've figured it out. You do need Bernoulli's equation. The pressure will be decreasing as you come in from the farthest out point of the arm. The rise in the water level will counteract this decrease in pressure. Now we just need to figure out the change in pressure going from the outside of the arm and working our way in.

An infinitesimal change in pressure from the dynamical pressure term (velocity pressure) will be:
$$dP= \rho_{air} v dv$$.

However, $$v=r\omega$$ and $$\rho_{air}=\frac{MP}{RT}$$
So we get:
$$dP=\frac{MPr\omega^2}{RT} dr$$
Rearrange and integrate:
$$\int_{P_0}^P \frac{dP'}{P'}=\int_l^0 \frac{M\omega^2 r}{RT} dr$$
which yields
$$P=P_0 exp(-\frac{M\omega^2 l^2}{2R T})$$
What I have found is the pressure in the air above the water inside the tube. Take the difference between this and $$P_0$$ and set it equal to $$\rho g h$$ (which is making up for the decrease in pressure) and you have the answer. Let me know if you see things wrong with my reasoning.