Physics 3-D Force Vector Question

[AIDB]

Homework Statement

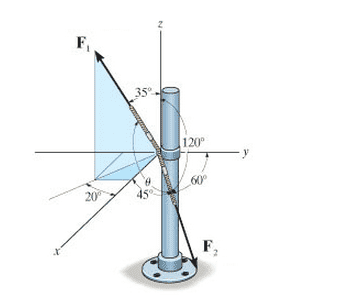
Determine the magnitude of the projected component of F1 along the line of action of F2, if the cables each exert a force of 410 N on the post.

The attempt at a solution

I know how to figure out F2x, F2y, and F2z, but I have no idea how to find F1y and F1x. Also, what does it mean by "F1 along the line of action of F2" and how would I give a final answer in that format?

Thank you

 

[debsankar]

For F1x and F1y , first calculate the projection on the given line in between x and -y >> G = F1 cos(90-35) then
F1x = G cos(20) and F1y = G cos(90+20) .
For F1 in the direction of F2 just take the dot product... (F1.F2)/ |F2|.

seems right to me, but please check with the angles and all...
Regards.

 

[Simon Bridge]

what does it mean by "F1 along the line of action of F2" and how would I give a final answer in that format?

Pretend that F2 is an axis - F1 has a component parallel to F2 and another one perpendicular to it.

Hint: what do dot and cross products do?

Note: debsankar has attempted to all-but do the problem for you - something that is usually unhelpful in the long-term. You should attempt to understand the approach used as well as applying it.