keydetpiper
- 3
- 0
In my high school physics class the other day the teacher botched an example problem involving sound level (decibels).
A single sound source produces 105 dB at a distance of 5.0 m. How far away must the observer be to not hear this sound at all?
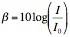
The reference intensity I0 is the lowest intensity a human can hear, 1 x 10-12 W/m2, so when the source is far enough away its intensity will be equal to this. The intensity of a sound falls off as 1/d2, so after substituting the information in the problem the equation above can be rewritten as follows:
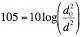
In this equation, d0 represents the distance to the sound source that produces the reference intensity and d is the distance to the original source, 5.0 m for this problem.
When this is solved for d0, the result is 177828d, or about 890 km. This can't be right! What happened? Thanks in advance for your help.
Homework Statement
A single sound source produces 105 dB at a distance of 5.0 m. How far away must the observer be to not hear this sound at all?
Homework Equations
The Attempt at a Solution
The reference intensity I0 is the lowest intensity a human can hear, 1 x 10-12 W/m2, so when the source is far enough away its intensity will be equal to this. The intensity of a sound falls off as 1/d2, so after substituting the information in the problem the equation above can be rewritten as follows:
In this equation, d0 represents the distance to the sound source that produces the reference intensity and d is the distance to the original source, 5.0 m for this problem.
When this is solved for d0, the result is 177828d, or about 890 km. This can't be right! What happened? Thanks in advance for your help.