Challenge How do you calculate the motion of a ball rolling on a rotating table?

[fresh_42]

TL;DR Summary

This is an experiment if we could establish a little physics competition.
Classical Physics, Special Relativity Theory

Problem 1 (@wrobel )
(solved by @TSny )

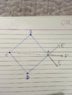
There is a perfectly rough horizontal table. This table is pretty wide (actually it is a plane) and it rotates about some vertical axis. Angular velocity is a given constant: $\Omega\ne 0$. Somebody throws a homogeneous ball on the table. The ball has a mass $m$ and a radius $r$.
The ball begins to roll on the table without slipping. Initially ($t=0$) a vector $\boldsymbol{OP}$ (see the picture) is known; initial angular velocity of the ball and initial velocity of its center of mass $S$ are also known vectors.
1) Prove that the center of the ball describes a circle relative to the lab frame;
2) Find the radius of this circle.

Problem 2 (@wrobel )
(solved by @TSny , @Chestermiller )

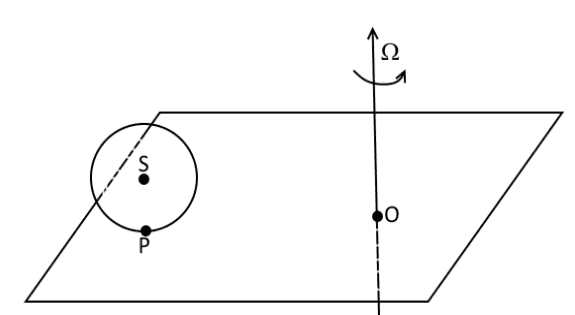
There are four homogeneous rods. Each rod has mass $m$ and length $b$. The ends of the rods are connected by frictionless hinges such that the rods form a rhombic frame (see the picture). This frame is shaped as square $ABCD$ and put at rest on a smooth horizontal table. Then one applies a force $F$ to the hinge $A$ along the diagonal #AC#. Find acceleration of the point $C$ right after the force has been applied.

Problem 3 (@PeroK )
(solved by @Gaussian97 )

a) Suppose a particle has three-velocity $\vec{u} = (u_x, u_y, u_z)$ in frame $S$, which is moving with velocity $(v, 0, 0)$ relative to frame $S'$. Show that the gamma factor of the particle in frame $S'$ is given by:
$$\gamma'_u = \gamma_v \gamma_u(1 + \frac{vu_x}{c^2})$$

b) Imagine a rig, consisting of two vertical poles, a distance $L$ apart. Two synchronised clocks are mounted on the poles and moving upwards at speed $u$, relative to the rig, remaining horizontally aligned with respect to the rig.

Imagine a frame of reference in which the whole rig is moving horizontally at speed $v$. By what amount are the clocks out of synchronisation in this frame?

c) Imagine instead that the clocks are aligned horizontally in the frame in which the whole rig is moving horizontally, as above. Note that the clocks are at rest relative to each other and assume they are synchronised in their own rest frame. By what amount are they out of synchronisation in the frame in which the rig is moving?

 

[Spinnor]

I tried to perform an experiment to show the conjectured circular orbit in the 1st problem above. My experiment can be seen here,



The results were suggestive but all my orbits were outward spirals. Question, we are told the sphere is homogenous, I assume that means it is a uniform solid sphere? Should we get the same results if the sphere is a uniform spherical shell?

Thanks.

If this gives too much away please delete.

 

[wrobel]

Should we get the same results if the sphere is a uniform spherical shell?

Yes. It is hard to provide the condition of non slipping in experiment

Little bit better: ball
simulation

 

[Spinnor]

Yes. It is hard to provide the condition of non slipping in experiment

Little bit better: ball
simulation

Same setup as above but not as "perfect" orbits,





Interesting if correct simulation,

This is interesting and beyond me but not Google. I wonder if there are solutions to this problem where the ball orbits at constant distance from the tables rotation center? Thank you for the puzzle.

 

[Gaussian97]

Problem 3:

Spoiler: Part a)

First of all, let me use a system of units where $c=1$. Then the four-velocity is defined as
$$u^\mu = \frac{d x^\mu}{d\tau} = \gamma_u\begin{pmatrix}1\\\vec{u}\end{pmatrix}$$
where $\vec{u}$ is the regular 3-velocity and $$\gamma_u \equiv \frac{1}{\sqrt{1-\vec{u}\cdot\vec{u}}}$$
so, for a particle with 4-velocity $u^\mu$ in a reference frame $\mathcal{S}$, the $\gamma$ factor is simply
$$\gamma_u = u^0$$.
Now, the Lorentz transformation to change from a RF $\mathcal{S}$ to another RF $\mathcal{S}'$, where $\mathcal{S}$ moves with velocity $\vec{v}=\begin{pmatrix}v\\0\\0\end{pmatrix}$ with respect $\mathcal{S}'$ is given by
$$\Lambda(\mathcal{S}'\leftarrow \mathcal{S})^{\mu}{}_{\nu} =
\begin{pmatrix}\gamma_v & v\gamma_v&0&0 \\ v\gamma_v & \gamma_v&0&0\\
0&0&1&0\\
0&0&0&1\\\end{pmatrix}$$

So, because $u^\mu$ is a contravariant tensor
$$\gamma_{u'}=u'^0=\Lambda(\mathcal{S}'\leftarrow \mathcal{S})^{0}{}_{\mu}u^\mu = \gamma_v u^0 + v\gamma_v u^1 = \gamma_v\gamma_u + v\gamma_v \gamma_u u_x = \gamma_v\gamma_u\left(1+vu_x\right)$$
Recovering the $c$ we are left with
$$\gamma_{u'} = \gamma_v\gamma_u\left(1+\frac{vu_x}{c^2}\right)$$

I'm not sure about b) and c), and if they are right, probably there is a better way to do it, but here is my attempt:

Spoiler: Parts b) and c)

The 4-position of the two clocks, in the RF of the left one (which I will call clock 1, while the other will be clock 2) are:
$$x_1^\mu(\tau)=\begin{pmatrix}\tau\\0\\0\\0\end{pmatrix}, \qquad x_2^\mu(\tau')=\begin{pmatrix}\tau'\\L\\y\\0\end{pmatrix}$$
Where $\tau, \tau'$ are the parametrizations of the worldlines. (I will keep an arbitrary $y$ by now.)
Then, in the rig reference frame ($\mathcal{S}$), which is related to the previous one by a $u$-boost
$$\Lambda^{\mu}{}_{\nu} =
\begin{pmatrix}\gamma_u & 0&u\gamma_u&0 \\ 0 & 1&0&0\\
u\gamma_u&0&\gamma_u&0\\
0&0&0&1\\\end{pmatrix}$$
the 4-positions are
$$x_{1,\mathcal{S}}^\mu(\tau)=\gamma_u\tau\begin{pmatrix}1\\0\\u\\0\end{pmatrix}, \qquad x_{2,\mathcal{S}}^\mu(\tau')=\begin{pmatrix}\gamma_u(\tau'+ uy)\\L\\\gamma_u(u\tau'+ y)\\0\end{pmatrix}$$
And, in the last RF ($\mathcal{S}'$), related to $\mathcal{S}$ by the LT in part a) the 4-positions are
$$x_{1,\mathcal{S}'}^\mu(\tau)=\gamma_u\tau\begin{pmatrix}\gamma_v\\v\gamma_v\\u\\0\end{pmatrix}, \qquad x_{2,\mathcal{S}'}^\mu(\tau')=\begin{pmatrix}\gamma_v(\gamma_u\tau'+ u\gamma_uy + vL)\\\gamma_v(v\gamma_u\tau'+ vu\gamma_u y + L)\\\gamma_u(u\tau'+ y)\\0\end{pmatrix}$$
The amount of desyncronization in the RF $\mathcal{S}'$ will be the difference $\Delta \tau = \tau'-\tau$ in a fixed time (so, under the condition $\Delta t=0$)
$$0=\Delta t = \gamma_v(\gamma_u\tau'+ u\gamma_uy + vL)-\gamma_u\tau\gamma_v \Longrightarrow \Delta \tau = -\frac{u\gamma_u y + vL}{\gamma_u}$$
with the clock 2 advanced an amount $\Delta \tau$.

Now, b) and c) are the same problem with different initial conditions $y$. The initial condition for b) is easy, simply we impose $y=0$, and the desynchronization is given by the previous expression
$$\Delta \tau = -\frac{vL}{\gamma_u} \rightarrow -\frac{vL}{\gamma_u c^2}$$

For c) we need to impose that the two clocks are horizontally aligned in $\mathcal{S}'$ which means that
$$0=\Delta y = \gamma_u(u\tau'+ y)-u\gamma_u\tau = u\gamma_u \Delta \tau + y \gamma_u \Longrightarrow yu\gamma_u = -u^2\gamma_u \Delta \tau$$
And therefore
$$\gamma_u\Delta \tau =u^2\gamma_u \Delta \tau -vL\Longrightarrow \Delta \tau = -\gamma_u vL\rightarrow -\gamma_u \frac{vL}{c^2}$$

In both cases, $v>0\Longrightarrow \Delta \tau <0$ so clock 2 will be delayed, while $v<0\Longrightarrow \Delta \tau > 0$ and clock 2 will be advanced.

 

[PeroK]

@Gaussian97 an impressive solution.

 

[Adesh]

An attempt at Problem 2

Spoiler

Due to geometry of masses we would center of mass at the Center of the square frame. The line of action of force and position vector are parallel therefore there will no torque (moment).
The force $F$ will cause a translation of COM, the whole frame will move and by Newton’s Law the acceleration felt by any particle on the body is $$ a = \frac{F}{4m}$. Hence, do the acceleration of point$C##.

 

[wrobel]

mmmmmmmmmm should I comment this? :)

 

[Adesh]

mmmmmmmmmm should I comment this? :)

Yes, please do comment.

 

[Spinnor]

The following is an approximate realization of problem 2. Please delete is it gives away too much.

 

[Adesh]

The following is an approximate realization of problem 2. Please delete is it gives away too much.

Did you fix your camera on your fan?

By the way thank you so much for the demonstration, I didn’t take into account that deformation of the frame was allowed. As far as I can think the point opposite to where the force is applied must accelerate away from the direction of force (due to formation).

 

[Spinnor]

Did you fix your camera on your fan?

By the way thank you so much for the demonstration, I didn’t take into account that deformation of the frame was allowed. As far as I can think the point opposite to where the force is applied must accelerate away from the direction of force (due to formation).

That was my first thought, the fan, but I found a microphone stand which you can make out a bit.

I think from the experiment there may be 3 different cases depending on the initial shape, squished one way, right angles, squished the other way?

 

[Adesh]

Spoiler: Question 2

We can break down the force $\vec{F}$ into components, one along AB and the other along AD.


Since, the diagonal of a square makes an angle of $45^{\circ}$ with its sides, therefore by geometry we would get $$ F_1 = F_2 = \frac{F}{\sqrt 2}$$.

SCENARIO 1
Force $F_2$ will cause AB to rotate anti-clockwise about its COM (which lies at its center). Moment produced by $F_2$ is $\frac{b~F}{2\sqrt 2}$. Let the angular momentum of the rod be denoted by $L$, then
$$ \frac{dL}{dt} = \frac{b~F}{2\sqrt 2} \\
\alpha = \frac{b~F}{2\sqrt 2 m} $$

The acceleration that point B will experience along BC (relative to COM of AB) is $$ a_{relative} = \alpha ~ b/2 \\ a_{relative} = \frac{b^2 ~F}{4\sqrt 2 m}$$
Acceleration of COM in a direction directly opposite to BC is $\frac{F}{\sqrt 2 m}$. So, actual acceleration of point B is $$ a_B = \frac{b^2 ~F}{4\sqrt 2 m} - \frac{F}{\sqrt 2 m} = \frac{F}{4\sqrt 2} (b^2-4)$$.

So, acceleration on point C along the direction of BC (B to C) is $a_B$. Force $F_1$ acts parallel to AB and will cause the rotation of the arm BC. Moment produced by $F_1$ on the arm BC is $\frac{b~F}{2\sqrt 2}$. Angular acceleration of BC $$ \frac{dL}{dt} = \frac{b~F}{2\sqrt 2} \\
\alpha = \frac{b~F}{2\sqrt 2 m} $$
Acceleration of point C (relative to COM of BC) along the direction of DC (D to C) is $$ a_{relative}= \frac{b^2 ~F}{4 \sqrt 2 m} $$ and the actual acceleration of point C is $$ a_c = \frac{b^2~F}{4\sqrt 2 m} - \frac{ F}{\sqrt 2 m} \\
a_c = \frac{F}{4\sqrt 2} (b^2 -4)$$
Free body diagram of arm BC:

Since, $a_c= a_B$, therefore the result acceleration will make an angle of 45 degrees with both $a_c$ and $a_B$ and hence the net acceleration of point C is along the diagonal AC (A to C) and it’s magnitude is $a_{net}=\frac{F}{4m} (b^2-4)$.

SCENARIO 2
Due to symmetry, the rotation of arms AD and CD will produce the same net acceleration on C and in the same direction.

FINAL ANSWER
So, the acceleration of the point C right after the force was applied is $$ a = \frac{F}{2m} (b^2-4) $$

 

[etotheipi]

Though doesn't the wording a force $F$ acts on the hinge imply a force of only $\frac{F}{2}$ on AB and AD each here (in addition to a vertical reaction force due to the hinge itself). And then also reaction forces due to the hinges at the other end?

 

[hutchphd]

b is a length, right?

 

[wrobel]

Solution of the problems implies the following two stages:

1) to write down differential equations of motion based on the laws and theorems of dynamics;

2) to provide a mathematically correct deduction of a result from the equations of motion.

 

[hutchphd]

Are we encouraged to point out issues, or would you prefer just solutions be submitted?

 

[Adesh]

Is my solution of problem 2 in post #13 incorrect ?

 

[hutchphd]

Is my solution of problem 2 in post #13 incorrect ?

The equation for α is dimensionally inconsistent as is the result.

 

[Adesh]

Error has been fixed, in post #13 I mistakingly took inertial mass instead of Moment of Inertia during the calculation of angular momentum.

Spoiler: Question 2

We can break down the force $\vec{F}$ into components, one along AB and the other along AD.
View attachment 261267

Since, the diagonal of a square makes an angle of $45^{\circ}$ with its sides, therefore by geometry we would get $$ F_1 = F_2 = \frac{F}{\sqrt 2}$$.

SCENARIO 1
Force $F_2$ will cause AB to rotate anti-clockwise about its COM (which lies at its center). Moment produced by $F_2$ is $\frac{b~F}{2\sqrt 2}$. Let the angular momentum of the rod be denoted by $L$, then
$$ \frac{dL}{dt} = \frac{b~F}{2\sqrt 2} \\
\alpha = \frac{6F}{\sqrt 2 mb}$$

The acceleration that point B will experience along BC (relative to COM of AB) is $$ a_{relative} = \alpha ~ b/2 \\ a_{relative} = \frac{3F}{\sqrt 2 m}$$
Acceleration of COM in a direction directly opposite to BC is $\frac{F}{\sqrt 2 m}$. So, actual acceleration of point B is $$ a_B = \frac{3F}{\sqrt 2 m} - \frac{F}{\sqrt 2 m} = \frac{\sqrt 2}{m}$$.

So, acceleration on point C along the direction of BC (B to C) is $a_B$. Force $F_1$ acts parallel to AB and will cause the rotation of the arm BC. Moment produced by $F_1$ on the arm BC is $\frac{b~F}{2\sqrt 2}$. Angular acceleration of BC $$ \frac{dL}{dt} = \frac{b~F}{2\sqrt 2} \\
\alpha = \frac{6F}{\sqrt 2 mb}$$
Acceleration of point C (relative to COM of BC) along the direction of DC (D to C) is $$ a_{relative}= \frac{3F}{\sqrt 2 m} $$ and the actual acceleration of point C is $$ a_c = \frac{3F}{\sqrt 2 m}- \frac{ F}{\sqrt 2 m} \\
a_c = \frac{\sqrt 2 F}{m}$$
Free body diagram of arm BC:
View attachment 261273
Since, $a_c= a_B$, therefore the result acceleration will make an angle of 45 degrees with both $a_c$ and $a_B$ and hence the net acceleration of point C is along the diagonal AC (A to C) and it’s magnitude is $a_{net}=\frac{2F}{m}$.

SCENARIO 2
Due to symmetry, the rotation of arms AD and CD will produce the same net acceleration on C and in the same direction.

FINAL ANSWER
So, the acceleration of the point C right after the force was applied is $$ a = \frac{4F}{m}$$

 

[wrobel]

Thus I see that there is no interest in this thread, so to finish with that the solution of the second problem is contained here https://www.physicsforums.com/threads/aceeleration-of-a-vertex.672835/#post-6331831

 

[Spinnor]

Thus I see that there is no interest in this thread

There is some interest, I pulled out my Engineering Dynamics book to study the relevant physics and at first could not understand the simplest simplification of this problem, a single rod with one end constrained to move on a line with a force applied to it, I think I get it now. In the process I think I know a little more and will give the 2nd problem one more try today (I promise I won't look at the solution.)

 

[Adesh]

Thus I see that there is no interest in this thread, so to finish with that the solution of the second problem is contained here https://www.physicsforums.com/threads/aceeleration-of-a-vertex.672835/#post-6331831

Problem 2 has taught me so many things that I think I could never learn from any book. The only problem was that I didn’t know Lagrangian Mechanics, although the problem could be solved by Newtonian Mechanics but solving it using NM wasn’t a good way.

I vote for physics challenge to be continued.

 

[etotheipi]

I think it's really hard to get the balance right with these sorts of challenges. I'm not quite too sure where the "Goldilocks" zone is!

Like Adesh said it'd be great to have something like this going, but it's a lot of effort on the problem setters' part and you'd want to make sure the thread was getting good traction. Either way, thanks to @wrobel and @PeroK for these questions!

 

[TSny]

PROBLEM 1

Spoiler: My attempt at problem 1

Let $\vec R_S$ be the position of the center of the ball relative to the origin $O$.

Let $\vec r$ be the position vector of $P$ relative to the center of the ball $S$. $\vec r$ always points vertically downward and has magnitude $r$ equal to the radius of the ball. So, $\vec r$ does not depend on time.

If $\vec \omega$ is the angular velocity of the ball about its center, then $S$ has velocity $\vec r \times \vec \omega$ relative to the rotating plane, assuming rolling without slipping. The rotation of the plane adds an additional amount to the velocity of $S$ relative to the lab. This additional amount is given by $\vec \Omega \times \vec R_s$. So, the velocity of $S$ relative to the lab is $$\vec V_S = \vec r \times \vec\omega + \vec \Omega \times \vec R_S$$

The acceleration of $S$ relative to the lab is

$$\vec a_S = \frac{d \vec V_S}{dt} = \vec r \times \frac{d \vec \omega}{dt} + \vec \Omega \times \frac{d \vec R_S}{dt}$$

$$\vec a_S = \vec r \times \vec \alpha + \vec \Omega \times \vec V_S $$

$\vec \alpha$ is the angular acceleration of the ball about its center $S$ and is due to the torque $\vec \tau = \vec r \times \vec f$, where $\vec f$ is the force of friction acting on the ball. If $I_S$ is the moment of inertia of the sphere about its center, $\vec \alpha = \frac{\vec r \times \vec f}{I_S}$.

So, $$\vec a_S = \frac { \vec r \times \left( \vec r \times \vec f \right)} {I_S} + \vec \Omega \times \vec V_S $$

Newton’s second law in the lab frame gives $\vec f = m \vec a_S$, where $m$ is the mass of the ball. Thus, $$\vec a_S = \frac {m}{I_S} \vec r \times \left( \vec r \times \vec a_S \right) + \vec \Omega \times \vec V_S $$

Note that $\vec r \times \left( \vec r \times \vec a_S \right) = -r^2 \, \vec a_S$ since $\vec a_S$ and $\vec r$ are perpendicular to each other. Hence, $$\vec a_S = -\frac {m r^2}{I_S} \vec a_S + \vec \Omega \times \vec V_S = -\frac{5}{2} \vec a_S + \vec \Omega \times \vec V_S $$ Here, we used $\frac {m r^2}{I_S} = \frac{5}{2}$ for a solid sphere.

Solving for $\vec a_S$, $$\vec a_S = \frac{2}{7} \vec \Omega \times \vec V_S $$

Thus, the acceleration of $S$ relative to the lab is always perpendicular to the velocity of $S$ relative to the lab. Since $\vec \Omega$ is constant, we may conclude that S moves in uniform circular motion relative to the lab. Letting $\rho$ denote the radius of the circular motion, $a_S= \frac{V_S^2}{\rho}$.

So, $$ \frac{V_S^2}{\rho} = \frac{2}{7} \Omega V_S $$

and, $$\rho = \frac{7}{2} \frac{V_s}{\Omega}$$.

The radius of the circular motion depends only on $\Omega$ and the speed $V_S$ of the ball relative to the lab.

Aside: The orbital angular speed of the circular motion is $\omega_{\rm orb} = V_s/\rho = \frac{2}{7} \Omega$. This appears to agree fairly well with what you see in the last video of post #4.

For a hollow sphere with $I_S = \frac{2}{3}mr^2$, one obtains $$\rho = \frac{5}{2} \frac{ V_s}{ \Omega}$$ So, in this case, $\omega_{\rm orb} = \frac{2}{5} \Omega$ , which agrees pretty well with the data at the end of the second video in post # 4 where a tennis ball was used.

 

[wrobel]

awesome! Problem 1 has been done by TSny

 

[Chestermiller]

My approach to problem 2 is very different from those presented so far. Like @Adesh, I too oriented CA along the x-axis and BC in the y direction. I then recognized that the loading on the structure could be resolved into two superimposable parts:

1. F/2 at A in the positive x-direction and F/2 at C in the positive x-direction
2. F/2 at A in the positive x-direction and F/2 at C in the negative x-direction

Loading 1 would result in the rigid body translation of the truss in the positive x direction with an acceleration of F/(4m).

Loading 2 would result in a pantographing of the truss, with stretching in the x-direction and contraction in the y-direction. This would result in both acceleration and rotation of each of the 4 members, and analysis of loading 2 for any of the 4 members would then comprise the bulk of the overall problem analysis. Vertex C would accelerate backwards relative to the center of mass.

If anyone is interested in the remainder of the analysis, I would be glad to provide it.

 

[Adesh]

If anyone is interested in the remainder of the analysis, I would be glad to provide it.

I’m, very much interested. I really need Newtonian Mechanics approach for this problem.

 

[Chestermiller]

I’m, very much interested. I really need Newtonian Mechanics approach for this problem.

OK. We already have the acceleration of the center of mass of the rhombic structure from Part 1 loading, so we are going to focus here exclusively on Part 2 loading. Our objective here will be to determine the acceleration of vertex A relative to the center of mass of the structure. The acceleration of vertex C relative to the center of mass of the rhombic structure will be minus the acceleration of vertex A.

We are going to be focusing on member AB, and will be analyzing the kinematics and dynamics of this member. First the kinematics. Let $\theta$ be the acute angle between member AB and the x-direction. In terms of this angle, the x-distance between the center of mass and vertex A is $b\cos{\theta}$ and the y-distance between the center of mass and vertex B is $b\sin{\theta}$. From this, it follows that the x-velocity of vertex A relative to the center of mass of the rhombus is $$v_{Ax}=-b\sin{\theta}\frac{d\theta}{dt}$$ and the y-velocity of vertex B relative to the center of mass of the rhombus is $$v_{By}=b\cos{\theta}\frac{d\theta}{dt}$$Differentiating again to get the accelerations, we have: $$a_{Ax}=-b\sin{\theta}\frac{d^2\theta}{dt^2}-b\cos{\theta}\left(\frac{d\theta}{dt}\right)^2$$and$$a_{By}=b\cos{\theta}\frac{d^2\theta}{dt^2}-b\sin{\theta}\left(\frac{d\theta}{dt}\right)^2$$At time zero, these accelerations reduce to $$a_{Ax}=-\frac{b}{\sqrt{2}}\frac{d^2\theta}{dt^2}$$and$$a_{By}=\frac{b}{\sqrt{2}}\frac{d^2\theta}{dt^2}=-a_{Ax}$$The accelerations of the center of mass of member AB relative to the center of mass of the rhombus are half these values, or $$a_{cmx}=\frac{a_{Ax}}{2}$$ and $$a_{cmy}=-\frac{a_{Ax}}{2}$$

Okay so far??

 

[Adesh]

In terms of this angle, the x-distance between the center of mass and vertex A is bcosθbcos⁡θb\cos{\theta} and the y-distance between the center of mass and vertex B is bsinθ

But can you please explain this part with the help of diagrams?

 

[etotheipi]

But can you please explain this part with the help of diagrams?

The centre of mass is at the centre of the rhombus. $\theta$ is the angle BAC.

 

[Chestermiller]

@Adesh
Hope this helps clear things up for you

FIGURE FOR PART 2 LOADING

 

[Adesh]

@Chestermiller Just one little doubt:

From this, it follows that the x-velocity of vertex A relative to the center of mass of the rhombus is

vAx=−bsinθdθdt​

How we got the minus sign?

 

[Adesh]

We can move on now. Everything is cleared till that far.

 

[Chestermiller]

@Chestermiller Just one little doubt:

How we got the minus sign?

The derivative of cosine is minus sine.

gotta stop now. Be back tomorrow.

 

[Chestermiller]

We can move on now. Everything is cleared till that far.

We next focus on the dynamics. This starts with the free body diagram for member AB:

View attachment 1588073847854.png
The above FBD shows the forces acting on strut AB. The tension F/4 at pin A is the portion of the imposted load F/2 that acts on strut AB. The tension R at pin A represents the contact force that strut DA imposes at A to keep vertex A from moving in the y direction. The tension T at pin B represents the contact force that strut CB imposes at B to pull vertex B back.

Next, we write the Newton's 2nd law force- and moment balances on strut AB. The force balances on AB in the x- and y-directions, respectively (based on the free body diagram) are:
$$\frac{F}{4}-T=ma_{cmx}=m\frac{a_{Ax}}{2}\tag{1}$$
$$-R=mA_{cmy}=-m\frac{a_{Ax}}{2}\tag{2}$$where use has been made here of some of the kinematic relations in post #29 to express the acceleration components of the center of mass of strut AB in terms of the x-direction acceleration of vertex A relative to the center of mass of the overall structure.

A clockwise moment balance on strut AB about its center of mass gives:
$$R\frac{b}{2\sqrt{2}}-\frac{F}{4}\frac{b}{2\sqrt{2}}-T\frac{b}{2\sqrt{2}}=I\frac{d^2 \theta}{dt^2}\tag{3}$$where I is the moment of inertial of the strut about its center of mass: $$I=m\frac{b^2}{12}\tag{4}$$If we combine Eqns. 3 and 4, we obtain:
$$R-\frac{F}{4}-T=\frac{m}{3}\frac{b}{\sqrt{2}}\frac{d^2 \theta}{dt^2}\tag{5}$$But, from post #29, $$\frac{b}{\sqrt{2}}\frac{d^2 \theta}{dt^2}=-a_{Ax}$$Therefore, $$\frac{F}{4}+T-R=\frac{m}{3}a_{Ax}\tag{6}$$
If we now combine Eqns. 1,2, and 6 to eliminate T and R, we obtain: $$a_{Ax}=\frac{3}{8}\frac{F}{m}$$Based on this and the results of Part 1 loading, we find that the absolute acceleration of vertex A is $\frac{F}{4m}+\frac{3}{8}\frac{F}{m}=\frac{5}{8}\frac{F}{m}$ and that the absolute acceleration of vertex C is $\frac{F}{4m}-\frac{3}{8}\frac{F}{m}=-\frac{1}{8}\frac{F}{m}$

 

[etotheipi]

@Chestermiller I had a question about your method. In the second part of your analysis you are using the fact that the behaviour of the system in the centre of mass frame is equivalent to having two opposite forces of F/2 on either side of the truss structure, causing it to pantograph.

I then recognized that the loading on the structure could be resolved into two superimposable parts:

1. F/2 at A in the positive x-direction and F/2 at C in the positive x-direction
2. F/2 at A in the positive x-direction and F/2 at C in the negative x-direction

I was wondering why it is possible to decompose the loading in this way? Superimposing all of those forces in their specified position indeed results in the same loading as in the problem statement, but why is it valid to only consider two of those forces at a time?

Essentially, why is the loading in the centre of mass frame only F/2 on each side? Since I'd presumed that in the accelerating centre of mass frame a fictitious F would act in the negative $x$ direction and the real F would act in the positive $x$ direction. Thanks!

 

[Adesh]

Thank you @Chestermiller

 

[wrobel]

I had a question about your method. In the second part of your analysis you are using the fact that the behaviour of the system in the centre of mass frame is equivalent to having two opposite forces of F/2 on either side of the truss structure, causing it to pantograph.

Yes indeed, I also have the same question. (Actually I have a lot of questions) Why is it F/2 that was applied not F/10 for example?

 

[Chestermiller]

@Chestermiller I had a question about your method. In the second part of your analysis you are using the fact that the behaviour of the system in the centre of mass frame is equivalent to having two opposite forces of F/2 on either side of the truss structure, causing it to pantograph.

I was wondering why it is possible to decompose the loading in this way? Superimposing all of those forces in their specified position indeed results in the same loading as in the problem statement, but why is it valid to only consider two of those forces at a time?

Essentially, why is the loading in the centre of mass frame only F/2 on each side? Since I'd presumed that in the accelerating centre of mass frame a fictitious F would act in the negative $x$ direction and the real F would act in the positive $x$ direction. Thanks!

The loading from Part 1 exactly cancels the pseudo body force resulting from the frame of reference acceleration. The Part 1 loading pushes from behind with a force of F/2 at C and pulls from the front with a force of F/2 at A. The reason I chose to resolve the superposition in the way that I did was because the Part 1 loading simply results in a rigid body translation of the truss and the Part 2 loading would simply result in pantographing.

 

[etotheipi]

The loading from Part 1 exactly cancels the pseudo body force resulting from the frame of reference acceleration. The Part 1 loading pushes from behind with a force of F/2 at C and pulls from the front with a force of F/2 at A. The reason I chose to resolve the superposition in the way that I did was because the Part 1 loading simply results in a rigid body translation of the truss and the Part 2 loading would simply result in pantographing.

I guess I'm just slightly confused about this method of superposition. I have never come across such an approach before. What allows us to break it down into a part 1 and a part 2 in the first place?

To my mind, we could either analyse this in the lab frame in which there is a sole force F acting at C, and zero external force at A. Or, we could transform into the centre of mass frame in which we still have a force F acting at C, in addition to a fictitious body force which essentially reduces to four forces of magnitude F/4 acting through the centres of mass of each of the rods, in the negative $x$ direction. In either of those frames, you could do force and torque analysis assuming you also draw the internal constraint forces between each of the rods on your free body diagram.

So then I'm not sure why it's permitted to first add on extra external forces at C, and secondly to consider two different scenarios in each of which only half of the forces act on the truss structure. Because neither part 1 nor part 2 represent the state of the system.

Thanks for your patience!

 

[Chestermiller]

I guess I'm just slightly confused about this method of superposition. I have never come across such an approach before. What allows us to break it down into a part 1 and a part 2 in the first place?

In my judgment, the equations for the two parts would be linearly superimposable to the overall equations.

To my mind, we could either analyse this in the lab frame in which there is a sole force F acting at C, and zero external force at A. Or, we could transform into the centre of mass frame in which we still have a force F acting at C, in addition to a fictitious body force which essentially reduces to four forces of magnitude F/4 acting through the centres of mass of each of the rods, in the negative $x$ direction. In either of those frames, you could do force and torque analysis assuming you also draw the internal constraint forces between each of the rods on your free body diagram.

So then I'm not sure why it's permitted to first add on extra external forces at C, and secondly to consider two different scenarios in each of which only half of the forces act on the truss structure. Because neither part 1 nor part 2 represent the state of the system.

Thanks for your patience!

Sorry, I don't think I can explain it any better than I did. However, I find it hard to believe that the analysis I presented could come up with exactly the correct answer if there were a fundamental flaw somewhere.

 

[etotheipi]

In my judgment, the equations for the two parts would be linearly superimposable to the overall equations.

This sort of makes sense to me though I don't really have a concrete picture of why it works. It appears to be a clever algebraic trick. It must be a valid method, though.

Just out of interest, do you know of any books or online resources which explain the general idea behind the superposition approach you took? It's an interesting idea.

 

[Chestermiller]

This sort of makes sense to me though I don't really have a concrete picture of why it works. It appears to be a clever algebraic trick. It must be a valid method, though.

Just out of interest, do you know of any books or online resources which explain the general idea behind the superposition approach you took? It's an interesting idea.

No. It's just something that popped into my head for this problem. I spent a lot of time thinking about this problem over several days before I arrived at this.

 

[Chestermiller]

I guess I'm just slightly confused about this method of superposition. I have never come across such an approach before. What allows us to break it down into a part 1 and a part 2 in the first place?

To my mind, we could either analyse this in the lab frame in which there is a sole force F acting at C, and zero external force at A. Or, we could transform into the centre of mass frame in which we still have a force F acting at C, in addition to a fictitious body force which essentially reduces to four forces of magnitude F/4 acting through the centres of mass of each of the rods, in the negative $x$ direction. In either of those frames, you could do force and torque analysis assuming you also draw the internal constraint forces between each of the rods on your free body diagram.

So then I'm not sure why it's permitted to first add on extra external forces at C, and secondly to consider two different scenarios in each of which only half of the forces act on the truss structure. Because neither part 1 nor part 2 represent the state of the system.

Thanks for your patience!

I thought about this some more. Try visualizing this problem: Suppose you had external forces of +F/2 in the positive x-direction at C and A. Would this guarantee that the truss translated as a rigid body? What would be the internal reaction forces at the ends of the struts? Suppose that you then looked at this from the center of mass frame of reference. It would be the same as having a gravitational body force acceleration g = F/(4m) acting in the negative x-direction, with the imposed forces at C and A acting to just balance the gravitation. OK so far?

 

[etotheipi]

It would be the same as having a gravitational body force acceleration g = F/(4m) acting in the negative x-direction, with the imposed forces at C and A acting to just balance the gravitation. OK so far?

That checks out, yes. OK so far!

 

[Chestermiller]

That checks out, yes. OK so far!

OK. Just so you're comfortable with this, what do you get for the reaction forces at the ends of the struts?

So now you have a truss situated in a gravitational field, with identical forces applied at its two ends to just hold it in equilibrium. This reminds me of a somewhat analogous situation of a mass in a gravitational field hanging in equilibrium at the end of a spring. You displace the mass vertically and then release it. Does the subsequent simple harmonic motion depend on g?

 

[etotheipi]

OK. Just so you're comfortable with this, what do you get for the reaction forces at the ends of the struts?

Suppose the truss is rigid. If you consider any single strut in the truss, there can be no $x$ component of reaction force at either hinge A or hinge C, due to reflection symmetry across the $x$ axis. The external force acting in the positive $x$ direction on each strut is is of magnitude F/4, which means that the $x$ component at B/D must also be zero for the correct $x$ acceleration of each strut. The $y$ components at each end of each strut must also be opposite forces. Torques about either A or C for the struts on either side of the $x$ axis mean these components have to be zero too. About the CM of each strut there is now a non-zero torque, which is a contradiction. So the truss is not rigid in this stage.

So now you have a truss situated in a gravitational field, with identical forces applied at its two ends to just hold it in equilibrium. This reminds me of a somewhat analogous situation of a mass in a gravitational field hanging in equilibrium at the end of a spring. You displace the mass vertically and then release it. Does the subsequent simple harmonic motion depend on g?

The motion is independent of $g$.

 

[Chestermiller]

Suppose the truss is rigid. If you consider any single strut in the truss, there can be no $x$ component of reaction force at either hinge A or hinge C, due to reflection symmetry across the $x$ axis. The external force acting in the positive $x$ direction on each strut is is of magnitude F/4, which means that the $x$ component at B/D must also be zero for the correct $x$ acceleration of each strut. The $y$ components at each end of each strut must also be opposite forces. Torques about either A or C for the struts on either side of the $x$ axis mean these components have to be zero too. About the CM of each strut there is now a non-zero torque, which is a contradiction. So the truss is not rigid in this stage.

This is correct with regard to the x-components, but not with regard to the y components. For strut AB, the y component of the reaction force imposed by strut BC at B is in the + y direction, and the y component of the reaction force imposed by strut DA at A is in the - y direction. These y direction forces are equal in magnitude. The couple created by these y-component reaction forces is equal and opposite to the couple associated with the x-gravitational force (at the center of mass) and the x imposed force at A. The x-forces are of magnitude F/4, and the magnitudes of the y reaction forces are F/8 (because of the larger moment arm). So there actually is a zero torque on the strut, and the truss does remain rigid.

 

[etotheipi]

These y direction forces are equal in magnitude. The couple created by these y-component reaction forces is equal and opposite to the couple associated with the x-gravitational force (at the center of mass) and the x imposed force at A. The

You're right, I concluded that the torques of the $y$ components canceled but of course they are both in the same sense.