tom23
- 4
- 0
Homework Statement
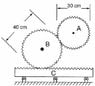
Gear ‘B’ on the machine shown below accelerates from rest to 250 rpm in 2 seconds. Determine the angular velocity and acceleration of A, and the linear acceleration and velocity of rack C. See image attached
Homework Equations
I don't know where i would start off with this question, help would be appreciated.