spinnaker
- 23
- 0
Kinda stumped. The question gives three equations and I don't know what to do with them, because given the equations there's always more than one unknown. Any assistance/tips would be appreciated!
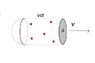
If a planetesimal has a cross-sectional area of πR2 (where R is the planetesimal's radius) and is sweeping through a cloud of smaller particles of fixed size with a velocity V, the number of collisions per second will be:
dn/dt = (πR2VρN)/m
where ρN=the space density (kg/m3) of particles in the cloud and m=the mass of each particle.
If each collision results in the target particles sticking to the planetesimal, the planetesimal will gain mass at a rate of
dM/dt = πR2VρN
where M=the planetesimal mass.
The time to grow to radius R is
t = (4R/V)/(ρP/ρN)
where ρP=the density of the planetesimal itself. (Assume that ρN and V stay constant as particles are swept up.)
Assuming that a reasonable value for the density of accretable material in inner part of the early solar nebula is ρN = 10-7 kg/m3, estimate the time to accrete a body of 1,000 km radius. Assume a reasonable ρP.
If a planetesimal has a cross-sectional area of πR2 (where R is the planetesimal's radius) and is sweeping through a cloud of smaller particles of fixed size with a velocity V, the number of collisions per second will be:
dn/dt = (πR2VρN)/m
where ρN=the space density (kg/m3) of particles in the cloud and m=the mass of each particle.
If each collision results in the target particles sticking to the planetesimal, the planetesimal will gain mass at a rate of
dM/dt = πR2VρN
where M=the planetesimal mass.
The time to grow to radius R is
t = (4R/V)/(ρP/ρN)
where ρP=the density of the planetesimal itself. (Assume that ρN and V stay constant as particles are swept up.)
Assuming that a reasonable value for the density of accretable material in inner part of the early solar nebula is ρN = 10-7 kg/m3, estimate the time to accrete a body of 1,000 km radius. Assume a reasonable ρP.