Please explain what is wrong with my relativistic momentum problem

[xox]

xox, I redid the computation as you told me - here is the result:

(Total momentum before on the left, total momentum after on the right)

u1, u2 - vertical components of balls` velocities before.
u3,u4 - vertical comoponents after

Sorry for not using special tegs. What I did is I added to u2 and u4 their horizontal components as they are given in the table.

Total before is still not equal to total after (they have opposite signs instead). What is wrong now?

This is definitely not what I have told you.

In the unprimed frame, before the collision:

p_{Ax}=\frac{mu_{Ax}}{\sqrt{1-\frac{u_{Ax}^2+u_{Ay}^2}{c^2}}}
p_{Ay}=\frac{mu_{Ay}}{\sqrt{1-\frac{u_{Ax}^2+u_{Ay}^2}{c^2}}}

p_{Bx}=\frac{mu_{Bx}}{\sqrt{1-\frac{u_{Bx}^2+u_{By}^2}{c^2}}}
p_{By}=\frac{mu_{By}}{\sqrt{1-\frac{u_{Bx}^2+u_{By}^2}{c^2}}}

You calculate the above y incorrectly because you are inadvertently dropping u_{x} in the calculation of your \gamma for p_{Ay}, p_{By}.

In the unprimed frame, after the collision:

p'_{Ax}=\frac{mu'_{Ax}}{\sqrt{1-\frac{u_{Ax}^{'2}+u_{Ay}^{'2}}{c^2}}}
p'_{Ay}=\frac{mu'_{Ay}}{\sqrt{1-\frac{u_{Ax}^{'2}+u_{Ay}^{'2}}{c^2}}}

p'_{Bx}=\frac{mu'_{Bx}}{\sqrt{1-\frac{u_{Bx}^{'2}+u_{By}^{'2}}{c^2}}}
p'_{By}=\frac{mu'_{By}}{\sqrt{1-\frac{u_{Bx}^{'2}+u_{By}^{'2}}{c^2}}}

You calculate the above y components incorrectly because you are inadvertently dropping u'_{x} in the calculation of your \gamma for p'_{Ay}, p'_{By}. You need to start to be able to figure out your mistakes on your own after so many explanations are given.

If you look at the calculations that Peter Donis did for you, using 4 vectors and you ignore the first component (in "t") you will notice the correct formulas. Hopefully, you will notice how his \gamma differs from yours.

 

[PAllen]

Probably I`m getting something absolutely wrong. Shouldn`t the following be the relativistic momentum formula?

p=\frac{mu}{\sqrt{1-(u/c)^2 }}

Can you now, please, just take velocity values from my table and substitute them into the equation correctly?

If by 'your table', you mean image 4 in you original post, I either don't understand it or disagree with it. The understanding issue is I still don't see where you define gamma and beta as used in those formulas. Also, in terms of simple (a,b) as defined in image 3, the Y coordinate velocity of ball 1 in S' should simply be:

b/√(1-a²)

(it's X coordinate velocity is zero, by construction, consistent with your image 4).

(In case it's unclear, I am taking (a,b) from your image 3 as given in units of c=1).

 

[Virous]

xox, that is exactly what I did. Your formulae:

Total momentum before:

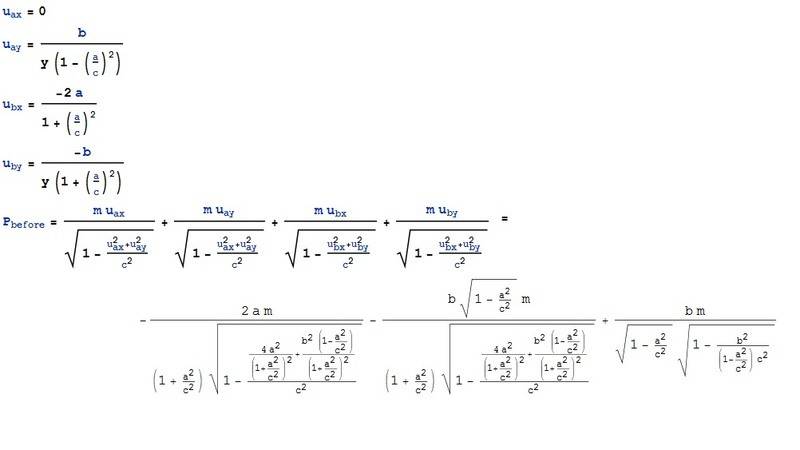
Total after:

It is absolutely clear, that they are not equal!

 

[Virous]

I`m sorry. Probably, I`m entirely stupid and can`t get a simple point. But it doesn`t bring me any closer to a solution of my problem.

 

[Virous]

PAllen, Beta is defined as (a/c) and gamma as (1-√(1-(a/c)^2) in ordinary units :)

 

[xox]

xox, that is exactly what I did. Your formulae:

Total momentum before:

Total after:

It is absolutely clear, that they are not equal!

Of course they are not, you are adding the x components with the y components, this is wrong. The conservation says:

p_{Ax}+p_{Bx}=p'_{Ax}+p'_{Bx}

p_{Ay}+p_{By}=p'_{Ay}+p'_{By}

Your p_{Before},p_{After} are wrong since you are adding the x and y components.

 

[Virous]

xox, if a=b and c=d, than a+c=b+d isn`t it?

P.S. In the second image it should be Pafter. Sorry :)

 

[xox]

xox, if a=b and c=d, than a+c=b+d isn`t it?

Yes, but this doesn't mean that you should be doing this. Try doing it on a component by component basis.

 

[Virous]

I tried many times in all the possible combinations. And as I told you before, x is conserved, but y is not. And my equations in the top show this. Because if a+b is not equal to b+d, as it is on the images, than there is no way for a to be equal to c together with b=d!

 

[xox]

I tried many times in all the possible combinations. And as I told you before, x is conserved, but y is not. And my equations in the top show this. Because if a+b is not equal to b+d, as it is on the images, than there is no way for a to be equal to c together with b=d!

Well, we found that your initial gammas were incorrect. Why don't you write the new equations on a component basis and we'll see easier what other mistake you may have.

 

[Virous]

If you get back to the very first post of mine, I have all the velocities in the primed frame in the table on Image 4. They are all calculated via relativistic addition formulae. Then, images I have in my previous post, just quoted by you are for primed frame. Unprimed frame is OK with me.

 

[xox]

Hello!

First, please, zoom in the attached file and take a look on it. Image 1 demonstrates the situation: two identical balls collide, horizontal component of velocity of both remains unchanged and vertical component becomes opposite as a result of the collision. Table in image 3 shows all the velocities in terms of a (horizontal component) and b (vertical).

Now we change the frame of reference into the one, which moves to the right on the speed of a. It is demonstrated on Image 2. New velocities are calculated via the relativistic velocity addition formula and are shown in the table on image 4.

Finally I calculated total momentum before (image 5) and total momentum after (image 6). Results are not equal! What did I do wrong?

http://stg704.rusfolder.com/preview/20140518/7/40730757_3_1176191.png

Deep thanks!

OK,

In the unprimed frame:

1. Before collision

\vec{u_A}=(a,b)
\vec{u_B}=(-a,-b)

2. After collision


\vec{u'_A}=(a,-b)
\vec{u'_B}=(-a,b)



Obviously the momentum before collision is equal to the momentum after collision:

p_{Ax}+p_{Bx}=p'_{Ax}+p'_{Bx}=0
p_{Ay}+p_{By}=p'_{Ay}+p'_{By}=0

If you get back to the very first post of mine, I have all the velocities in the primed frame in the table on Image 4. They are all calculated via relativistic addition formulae. Then, images I have in my previous post, just quoted by you are for primed frame. Unprimed frame is OK with me.

Yes, but we found out that your "gammas" were incorrect. Using the corrected "gammas", try writing the speeds and the equations of momentum conservation (as I did above) as measured from the boosted frame. Please do not mix the components, this makes error detection more difficult. BTW, I found another error, your Image 5,6 do not represent the "total momentum", you are missing one term in both "before" and "after". There should be 3 terms, not 2.

 

[Virous]

I don`t get where are they incorrect. So what are the correct equations?

 

[xox]

I don`t get where are they incorrect. So what are the correct equations?

You need to learn how to find out the errors, work, do not expect us to do all the work for you.

 

[Virous]

I do not expect anyone to do anything for me. I spent a weekend trying to solve this. Everything I reached I already posted. I have no idea, where my errors are. That is why I`m here.

 

[Virous]

POST #56 has my calculations. Just, please, point out where the mistake is.

 

[Virous]

Again, the book says, that it is entirely straight forward. As we see, it is so straight forward, that 6 people can`t solve it on 4 pages of the forum :)

 

[xox]

I do not expect anyone to do anything for me. I spent a weekend trying to solve this. Everything I reached I already posted. I have no idea, where my errors are. That is why I`m here.

You need to redo some of the calculations and post them. I pointed out the calculations that need to be redone and how to redo them.

 

[xox]

Again, the book says, that it is entirely straight forward. As we see, it is so straight forward, that 6 people can`t solve it on 4 pages of the forum :)

Actually, Peter Donis solved it all for you. And I spent a lot of time pointing out your mistakes. We are not supposed to do your homework, you need to learn how to do it right.

 

[Virous]

It is not a homework. It is my own attempt to get into mathematics of special relativity. If it was a homework, I would ask the person who gave it to me :)

Yes, I saw the solution of Peter Donis. However, I need to understand the mistake in my one, since I don`t believe, it`s a good idea to take different approach, until you understand, what`s the problem with the first one.

All of my calculations are already posted. I`ll go through them once more...

So, what we have initially is this:

This table shows the velocities of two balls before and after collision in terms of their vertical and horizontal components. That is how it happens in frams S.

Now we move to another frame S', which moves to the right with velocity of a. Recalculating of velocities gives:

This table was taken directly from the book (however, I checked it for errors several times and from my point of view it is fully correct). In this table gamma stands for \frac{1}{\sqrt{1-(\frac{a}{c})^2}} and beta stands for a/c.

Now I tried to calculate momenta before and after. And what I did (by substitution to xox`s formulas) I have on these two images:

Before:

After:

It is clearly visible, that momenta are not conserved. I do not understand why.

 

[Virous]

I`m very sorry for taking your time. You said, that I`m omitting x components. I included them in the way you showed me. If I did it incorrectly, please, tell me where.

 

[Virous]

Without x components of momenta:

 

[Virous]

After:

 

[xox]

I`m very sorry for taking your time. You said, that I`m omitting x components. I included them in the way you showed me. If I did it incorrectly, please, tell me where.

Yes, you corrected that error. You also corrected the fact that you were missing one term in your first post. Now, stop being so stubborn and separate the equation of conservation into the x and y components, as I showed you. You have a sign error someplace but it is very difficult to debug since you insist on adding the x and y components of the momentum.

 

[Virous]

Just forget about x-components. They are fine. Y components are just the two posts above your last one.

 

[xox]

Just forget about x-components. They are fine. Y components are just the two posts above your last one.

This is better, now please put the "before" and "after" in one post, so I can compare the results.

 

[Virous]

Sure!

Before:

After:

 

[PeterDonis]

Virious, your $u_{by}$ values are wrong; the denominator should have $\left( 1 - (a / c )^2 \right)$, not $\left( 1 + (a / c)^2 \right)$.

Also, you really need to learn to use the forum LaTeX feature to write equations, instead of posting images. Check out this guide:

https://www.physicsforums.com/showpost.php?p=3977517&postcount=3

 

[Virous]

PeterDonis, Ball B moves in the negative direction in frame S and frame S' moves in the positive. Hence we have (-a)*(a) which gives -a^2. And - times - gives +

 

[Virous]

Yes, yes, sorry about LaTeX. I`m using it whenever I can. But because I have all of these equations in Wolfram Mathematica, I just screenshot them to save time. They are quite huge and it will take a lot to copy them. Sorry again!

 

[Virous]

To derive these equations (in the table) I used velocity addition formula:

u'=\frac{u}{\gamma (1-\frac{u_{x}v}{c^2})}

v here is a velocity of S' in S. It is a.
ux is -a, since Ball B moves to the left.
uy is -b.

If you`ll substitute, you`ll get the denominator with "+"

 

[Virous]

Wow, your previous post just disappeared :)

 

[xox]

Sure!

Before:

After:

OK, it is getting close, we are down to an apparent sign inversion between "before" and "after" total momentum.

Now, I will give you a hint: look at the first term in the "before" and work the expression under the radical

(1+\frac{a^2}{c^2})^2-4\frac{a^2}{c^2}-\frac{b^2}{c^2}(1-\frac{a^2}{c^2})=(1-\frac{a^2}{c^2})(1-\frac{a^2}{c^2}-\frac{b^2}{c^2})

 

[PeterDonis]

PeterDonis, Ball B moves in the negative direction in frame S and frame S' moves in the positive. Hence we have (-a)*(a) which gives -a^2. And - times - gives +

Actually, looking back at my post #37, I was wrong. The correct values for $u_{ay}$ and $u_{by}$ before (the only change in the after values is that the signs are swapped) are, as I noted in an earlier post, the ratios $u^y / u^t$ of the values from my post. Those are (again, I'm using units where $c = 1$):

$$
u_{ay} = \frac{b}{\sqrt{1 - a^2}}
$$

$$
u_{by} = \frac{- b \sqrt{1 - a^2}}{1 + a^2}
$$

So the corresponding momentum values are (note that I'm using your values for $u_{ax}$ and $u_{bx}$, which are correct):

$$
p_{ay} = \frac{m u_{ay}}{\sqrt{1 - u_{ax}^2 - u_{ay}^2}} = \frac{m b}{\sqrt{1 - a^2} \sqrt{1 - b^2 / \left( 1 - a^2 \right)}} = \frac{m b}{\sqrt{1 - a^2 - b^2}}
$$

$$
p_{by} = \frac{m u_{by}}{\sqrt{1 - u_{bx}^2 - u_{by}^2}} = \frac{- m b \sqrt{1 - a^2}}{\left( 1 + a^2 \right) \sqrt{1 - \left( 2 a \right)^2 / \left( 1 + a^2 \right)^2 - b^2 \left( 1 - a^2 \right) / \left( 1 + a^2 \right)^2}} = \frac{- m b}{\sqrt{\left[ \left( 1 + a^2 \right)^2 - 4 a^2 \right] / \left( 1 - a^2 \right) - b^2}} = \frac{- m b}{\sqrt{1 - a^2 - b^2}}
$$

So the $y$ momentum does cancel, as desired.

 

[Virous]

It was like this even before all the corrections :) The point is, that if we use the classical momentum formula (p=mu), we get this error. Introduction of gamma according to the book must solve this problem, but it doesn`t.

 

[PeterDonis]

Introduction of gamma according to the book must solve this problem, but it doesn`t.

Check my post #84, your $y$ velocity components were indeed wrong, I just gave a mistaken correction previously.

 

[xox]

It was like this even before all the corrections :) The point is, that if we use the classical momentum formula (p=mu), we get this error. Introduction of gamma according to the book must solve this problem, but it doesn`t.

This is not the issue, you haven't finished your calculations, use the hint I gave you, some very nice simplification will happen.

 

[Virous]

Your hint didn`t exist, when I saw your post the first time. Sorry :(

 

[xox]

Your hint didn`t exist, when I saw your post the first time. Sorry :(

post 83, you are very close, if you do the calculations correctly you should get the total momentum to be null.

 

[Virous]

Oh, yeeeeees! I found it! It simplifies to zero. My problem was, that I fully relied on my Math software, and it for some reason didn`t simplified it completely, because of possiblity of imaginary roots in case of overcoming the speed of light!

Thanks to everyone! So, summarizing everything, my initial mistake was in the fact, that I had to add velocity components geometrically via pyphagora`s theorem!

Thanks to all!

 

[xox]

Oh, yeeeeees! I found it! It simplifies to zero. My problem was, that I fully relied on my Math software, and it for some reason didn`t simplified it completely, because of possiblity of imaginary roots in case of overcoming the speed of light!

Thanks to everyone! So, summarizing everything, my initial mistake was in the fact, that I had to add velocity components geometrically via pyphagora`s theorem!

Thanks to all!

Yes, you had the "gammas" computed incorrectly, this and the fact that you did not persevere enough, were your only flaws.
On an amusing note, humans are still better than software, your tool was incapable of detecting the expression simplification. Out of curiosity, what software are you using?

 

[Virous]

It was. The problem was, that if the speed is bigger than the speed of light, simplification won`t work (because of imaginary numbers). Since the software had to consider all the cases, it stopped there. It worked well after I added a<c and b<c into assumptions list.

I`m using Wolfram Mathematica.

 

[xox]

It was. The problem was, that if the speed is bigger than the speed of light, simplification won`t work (because of imaginary numbers). Since the software had to consider all the cases, it stopped there. It worked well after I added a<c and b<c into assumptions list.

I`m using Wolfram Mathematica.

interesting...this is a rather spectacular failure to complete a simple symbolic computation, the result is 0 , you shouldn't be forced to add the conditions a<c and b<c. I think those fabled East Europeans coding Mathematica are not that hot after all :-)

 

[PAllen]

One thing that I see caused me confusion was terminology (either from the book or Virous, not sure). The formulas given for deriving image 4 in the OP are just Lorentz transform of coordinate velocities. They are not velocity addition formulas in the sense I was thinking. In the case of all x motion, the Lorentz transform for Ux is, of course, the simplest velocity addition formula. In all other cases, they don't give you the resultant speed or gamma (as the formula I gave does). They just give you components in the frame boosted by v in the x direction. You then have to compute resultant speed and gamma.

[Virous: is that a British virus? ]

 

[xox]

Virious, your $u_{by}$ values are wrong; the denominator should have $\left( 1 - (a / c )^2 \right)$, not $\left( 1 + (a / c)^2 \right)$.

Also, you really need to learn to use the forum LaTeX feature to write equations, instead of posting images. Check out this guide:

https://www.physicsforums.com/showpost.php?p=3977517&postcount=3

No, his speeds are transformed correctly, his only errors were:

-incorrect formula for some of the "gammas"

-relying on Mathematica to do the final simplification of the expressions (Mathematica failed in a spectacular way)

I have encountered some failures in Matlab but never before in Mathematica. This was an interesting experience.

 

[PeterDonis]

No, his speeds are transformed correctly

Yes, you're right, he expressed them differently, but looking again at his expressions they are equivalent to mine.

 

[xox]

[Virous: is that a British virus? ]

A Russian one.

 

[Virous]

A Russian one.

How do you know that? :)

(my articles, probably) :D

 

[xox]

How do you know that? :)

(my articles, probably) :D

Yep.

 

[Virous]

I have encountered some failures in Matlab but never before in Mathematica. This was an interesting experience.

This is not a failure. It should be like this, since the conservation law does not work for speeds >c.

Final results (everything works, assuming, that a+b<c geometrically):