- #1
tracker890 Source h
- 90
- 11
No Effort - Member warned that some effort must be shown
Dear Everyone:
Q:Please help me to understand how to solve the P(theta)min is
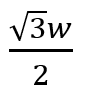 ?
?
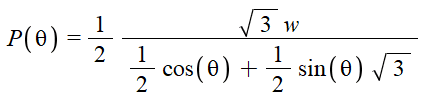
Thank you for your time and consideration.
Q:Please help me to understand how to solve the P(theta)min is
Thank you for your time and consideration.