I Plotting the orbits of the planets

[Astro Student]

Hello everybody! Long-time lurker and second-time posting. I'm working on a project for my math class, and I'm trying to plot the orbits of the planets using vectors. I've chosen to use MATLAB because I am decently familiar with it. I've used the formulas described in this post here to get my function for the program, and this website here for the data by clicking on the names of each planet and scrolling down to the "orbital elements" section.

For some reason, things look quite a bit off. Here's a screenshot of what I mean:

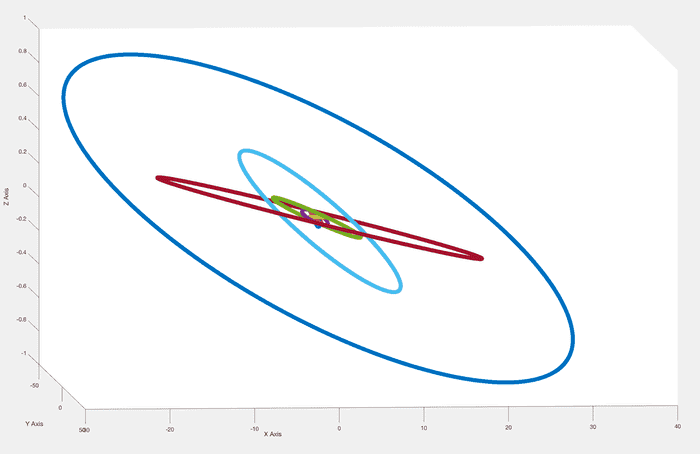
The planes of the orbits just don't seem like they are very similar at all! I don't recall them ever being like that.

Along the x-y plane, however, things seem to be going great:

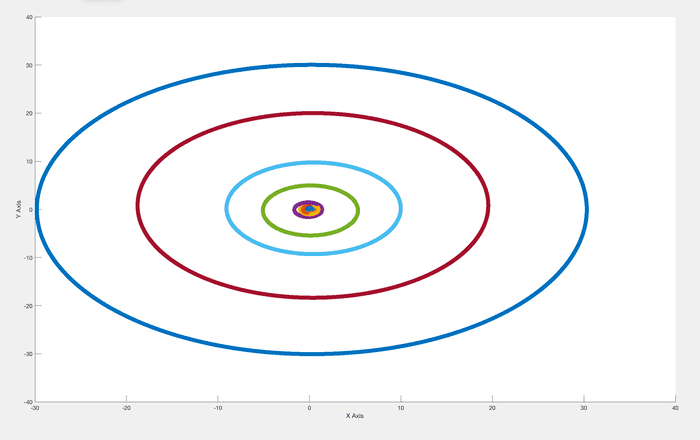
As seen here, my problem seems to be MOSTLY with the terrestrial planets. Earth, in orange, is pretty messed-up looking. Jupiter, in green, is on a similar plane to Saturn, Uranus, and Neptune otherwise.

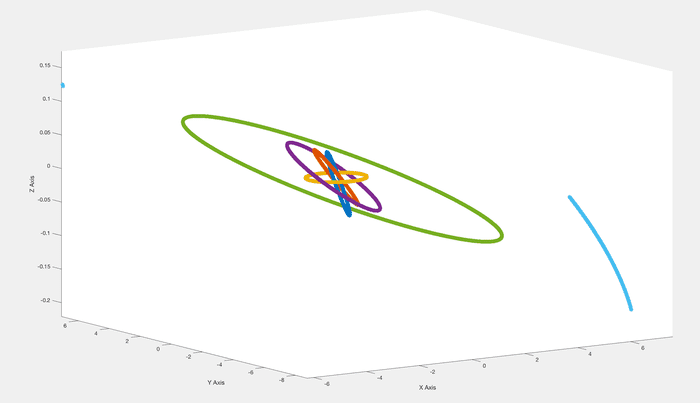
As far as I can tell, I've done everything correctly. If anybody has any ideas at all or can help me, please let me know! Thanks.

Here's my code:

%Graphs!

%Define Mercury's parameters
a(1) = 0.38709893; %semi-major axis
e(1) = 0.20563069; %eccentricity
i(1) = 7.00487 * (pi/180); %inclination relative to ecliptic
inv(1) = 6.34 * (pi/180); %inclination relative to invariable plane
w(1) = 77.45645 * (pi/180); %argument of periapsis
o(1) = 48.33167 * (pi/180); %longitude of ascending node

%Define Venus' parameters
a(2) = 0.72333199;
e(2) = 0.00677323;
i(2) = 3.39471 * (pi/180);
inv(2) = 2.19 * (pi/180);
w(2) = 131.53298 * (pi/180);
o(2) = 76.68069 * (pi/180);

%Define Earth's parameters
a(3) = 1.000001;
e(3) = 0.01671123;
i(3) = 0 * (pi/180);
inv(3) = 1.57 * (pi/180);
w(3) = 102.94719 * (pi/180);
o(3) = -11.26064 * (pi/180);

%Define Mars' parameters
a(4) = 1.52366231;
e(4) = 0.09341233;
i(4) = 1.85061 * (pi/180);
inv(4) = 1.67 * (pi/180);
w(4) = 336.04084 * (pi/180);
o(4) = 49.57854 * (pi/180);

%Define Jupiter's parameters
a(5) = 5.20336301;
e(5) = 0.04839266;
i(5) = 1.30530 * (pi/180);
inv(5) = 0.32 * (pi/180);
w(5) = 14.75385 * (pi/180);
o(5) = 100.55615 * (pi/180);

%Define Saturn's parameters
a(6) = 9.53667594;
e(6) = 0.05386179;
i(6) = 2.48599187 * (pi/180);
inv(6) = 0.93 * (pi/180);
w(6) = 92.59887831 * (pi/180);
o(6) = 113.66242448 * (pi/180);

%Define Uranus' parameters
a(7) = 19.18916464;
e(7) = 0.04725744;
i(7) = 0.77263783 * (pi/180);
inv(7) = 1.02 * (pi/180);
w(7) = 170.95427630 * (pi/180);
o(7) = 74.01692503 * (pi/180);

%Define Neptune's parameters
a(8) = 30.06992276;
e(8) = 0.00859048;
i(8) = 1.77004347 * (pi/180);
inv(8) = 0.72 * (pi/180);
w(8) = 44.96476227 * (pi/180);
o(8) = 131.78422574 * (pi/180);

%initialize arrays
x(1,1,1) = 0;
y(1,1,1) = 0;
z(1,1,1) = 0;

%Find the eccentric anomaly for 'plottedPloints' amounts of times
plottedPoints = 10000;
M(1) = 0; %mean anomaly vector
E(1,1,1) = 0; %eccentric anomaly array
iterations = 100; %number of iterations through for E(t)

for t = 1 : plottedPoints %create points for our mean anomaly
    M(t) = (2*pi*t)/plottedPoints;
end

for p = 1 : 8
    for t = 1 : plottedPoints
        E(p,1,t) = M(t);
        for k = 1 : iterations - 1
            E(p,k+1,t) = M(t) + e(p)*sin(E(p,k,t));
        end
    end
end

%Find our position vectors!
for p = 1 : 8
    for t = 1 : plottedPoints
        x(p,1,t) = a(p) * (cos(E(p,iterations,t)) - e(p));
        y(p,1,t) = a(p) * power((1 - power(e(p),2)),0.5) * sin(E(p,iterations,t));
        z(p,1,t) = 0;
 
        x(p,2,t) = x(p,1,t)*cos(w(p)) - y(p,1,t)*sin(w(p));
        y(p,2,t) = y(p,1,t)*cos(w(p)) + x(p,1,t)*sin(w(p));
        z(p,2,t) = z(p,1,t);
 
        x(p,3,t) = x(p,2,t);
        y(p,3,t) = y(p,2,t)*cos(i(p));
        z(p,3,t) = y(p,2,t)*sin(i(p));
 
        x(p,4,t) = x(p,3,t)*cos(o(p)) - y(p,3,t)*sin(o(p));
        y(p,4,t) = x(p,3,t)*sin(o(p)) + y(p,3,t)*cos(o(p));
        z(p,4,t) = z(p,3,t);
    end
end

%i don't know away around this, but i am just creating a bunch of vectors
%since i can't use them directly
for t = 1 : plottedPoints
    mercuryx(t) = x(1,4,t);
    mercuryy(t) = y(1,4,t);
    mercuryz(t) = z(1,4,t);
 
    venusx(t) = x(2,4,t);
    venusy(t) = y(2,4,t);
    venusz(t) = z(2,4,t);
 
    earthx(t) = x(3,4,t);
    earthy(t) = y(3,4,t);
    earthz(t) = z(3,4,t);
 
    marsx(t) = x(4,4,t);
    marsy(t) = y(4,4,t);
    marsz(t) = z(4,4,t);
 
    jupiterx(t) = x(5,4,t);
    jupitery(t) = y(5,4,t);
    jupiterz(t) = z(5,4,t);
 
    saturnx(t) = x(6,4,t);
    saturny(t) = y(6,4,t);
    saturnz(t) = z(6,4,t);
 
    uranusx(t) = x(7,4,t);
    uranusy(t) = y(7,4,t);
    uranusz(t) = z(7,4,t);
 
    neptunex(t) = x(8,4,t);
    neptuney(t) = y(8,4,t);
    neptunez(t) = z(8,4,t);
end

figure
plot3(mercuryx,mercuryy,mercuryz,'*',venusx,venusy,venusz,'*',earthx,earthy,earthz,'*',marsx,marsy,marsz,'*',jupiterx,jupitery,jupiterz,'*',saturnx,saturny,saturnz,'*',uranusx,uranusy,uranusz,'*',neptunex,neptuney,neptunez,'*')
xlabel('X Axis')
ylabel('Y Axis')
zlabel('Z Axis')

 

[phyzguy]

It looks to me like it's OK. Notice that it autoscales the plots, so the z-axis scale is magnified more than 10X compared to the X and Y axis scales. So you are seeing the small inclinations of the orbits. Try scaling the plots so the X, Y and Z axes scales are all the same.

 

[Astro Student]

It looks to me like it's OK. Notice that it autoscales the plots, so the z-axis scale is magnified more than 10X compared to the X and Y axis scales. So you are seeing the small inclinations of the orbits. Try scaling the plots so the X, Y and Z axes scales are all the same.

Ahhh I never thought Matlab would do such a thing to me! Thank you very much, everything looks great now that I've set my own scales!

As an aside would you or anybody else happen to know why Earth has a longitude of ascending node -11.26064 degrees? If this were true, then what the heck is our 'ecliptic'? My only thought is that it could be an adjustment relative to the invariable plane, but then the inclinations on the NASA site wouldn't make sense since they are, in fact, relative to our ecliptic.

Thanks again!