Plotting the Poynting vector of a radiating electric dipole [matlab]

[PhDeezNutz]

I found out why my lines were disappearing; In each iteration of the for loop the contours are re-calibrated so to speak. To counteract that I set the scale at t = 0 and used that "set in stone scale" inside the for loop to "keep everything uniform" and make the wave look like it's traveling continuously.

Here's the result which has a few problems:

1) There's contours on the dipole axis

2) For some reason everything is real slow, I've tried changing frame rates in the range from 20 to 1000. no dice.

On the plus side

3) The radiation pattern seems to be contained within a constant "envelope" and parts of that envelope are not disappearing thankfully. Hopefully this is not a coincidence of doing something wrong.

Strangely when I use a website to convert my mp4 to a gif the gif actually turns out alright; it has a non vanishing envelope and isn't super slow. My mp4 is terrible.

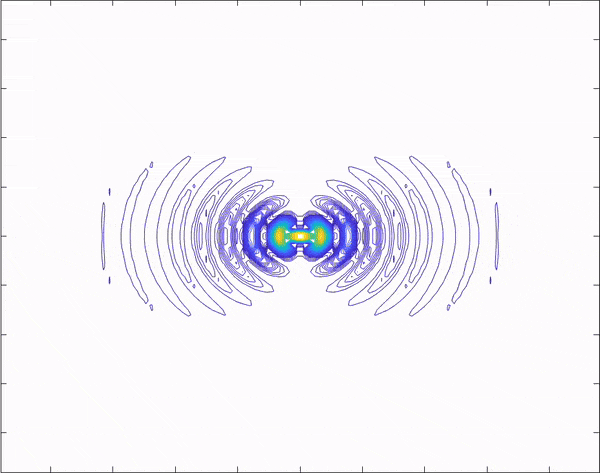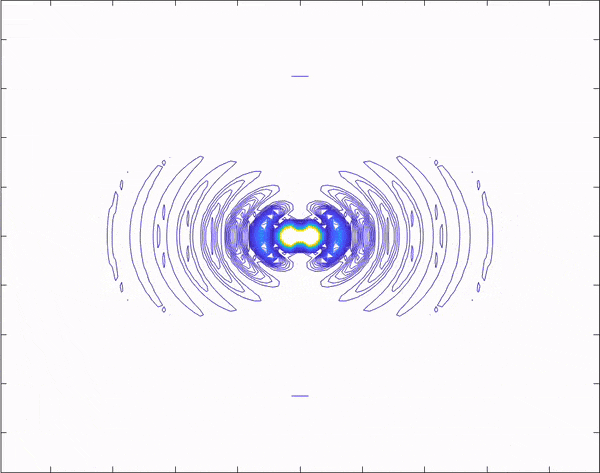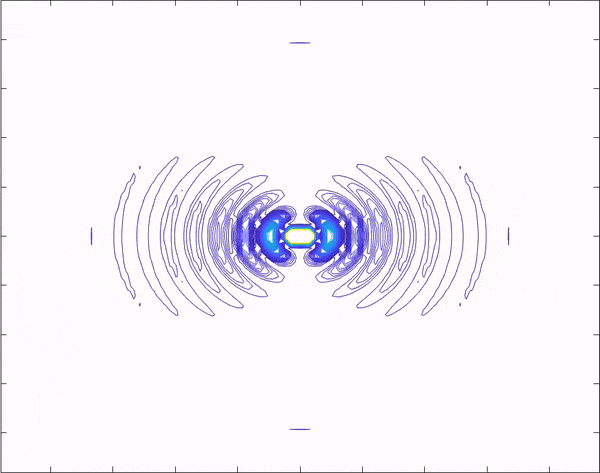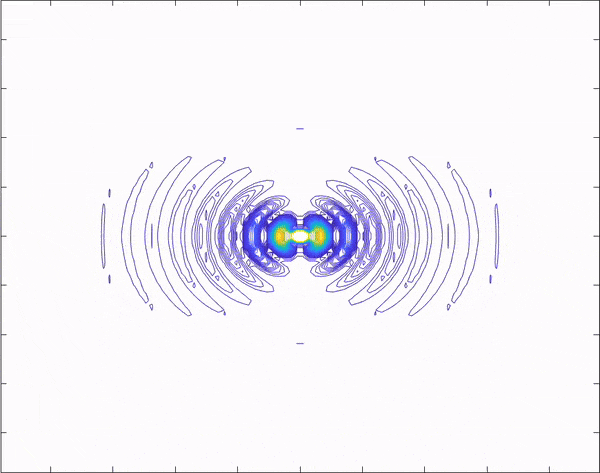
edit: actually when opening my mp4 in a separate player it turns out fine. but the contours on the dipole axis are concerning.

 

[TSny]

Looks nice. The contours along the axis of the dipole are interesting. The magnitude of S is zero at all points exactly on the axis. For points near the axis, but not on the axis, S will be small but nonzero. So, if you are plotting contours with small values, then you can get some contours near the axis.

Here is a plot of contour lines near the positive z-axis over a range of about 2 to 5 wavelengths from the dipole. They seem to have some interesting strucure.

The two graphs below zoom in on this region at about 4.75 wavlengths from the dipole

 

[PhDeezNutz]

I followed your advice and filtered the smallest number from the range of S magnitudes and now the contours on the dipole axis are gone.

I have a special relativity presentation due Tuesday do you think I could incorporate this somehow? Perhaps boost it to another "nearly c" frame and see how it looks. What should I expect in such a case? (depending on which direction I boost in). I'm just thinking out loud here. I just want an excuse to continue working on this script.

(I bet that's a loaded question)

Edit: I think Jackson page 558 has the answers

 

[TSny]

Your movies are looking pretty good!

I have a special relativity presentation due Tuesday do you think I could incorporate this somehow? Perhaps boost it to another "nearly c" frame and see how it looks. What should I expect in such a case? (depending on which direction I boost in).

Yes, the radiation pattern of a relativistically moving, radiating dipole could be interesting. If the dipole moves in a direction that is perpendicular to the axis of oscillation, I think you should see some "bunching" of the contour lines out in front of the dipole corresponding to the Doppler effect. Also, it could be that the strength of the Poynting vector is increased in the forward direction. That is, maybe the radiation gets "beamed forward" at relativistic speeds.

Edit: I think Jackson page 558 has the answers

Yes, here you have the transformation equations for the fields when switching frames of reference.

 

[PhDeezNutz]

Your movies are looking pretty good!

Thank you! I couldn't have done it without your help.

Yes, the radiation pattern of a relativistically moving, radiating dipole could be interesting. If the dipole moves in a direction that is perpendicular to the axis of oscillation, I think you should see some "bunching" of the contour lines out in front of the dipole corresponding to the Doppler effect. Also, it could be that the strength of the Poynting vector is increased in the forward direction. That is, maybe the radiation gets "beamed forward" at relativistic speeds.

Yes, here you have the transformation equations for the fields when switching frames of reference.

I'll look for these patterns when making the script. I'll update this thread when I get somewhere with it.

After that my plan is to generalize my dipole script to something like the following so that I can eventually handle the quadrupole (coming up with analytical expressions for this might be hard but I hardly know anything about Finite Element Analysis so I have to come up with analytical expressions).

 

[PhDeezNutz]

@TSny If I transformed the field correctly. I'm traveling at 0.9c along the y - axis (with the dipole along the z-axis)

and I get the following

I don't know what to make of it to be honest.

Is it correct/what you would expect?

Again, I'm traveling fast in a direction perpendicular to the dipole (the y-direction with the dipole along the z-direction) and I'm constraining the poynting vector intensity to the xz-plane.

I'm using the same color spectrum as my previous script.

It seems very strange that radiation would be perpendicular to the direction it was previously in.

 

[TSny]

The animation doesn't look correct to me.

Suppose the primed frame is the frame in which the dipole is at rest. In the unprimed frame, the dipole moves along the y-axis. At the instant the dipole crosses the xz plane in the unprimed system, you can consider the value of the Poynting vector at each point of the xz plane. If you ignore $S_y$ and plot the contour lines of $\sqrt{S_x^2 + S_z^2}$ in the xz plane, I think you will get the same pattern of contours as for a dipole at rest. I find that the only difference is that the value of a particular contour in the xz plane for the moving dipole is greater by the gamma factor $\gamma$ compared to the same contour when the dipole is at rest. In other words, $\sqrt{S_x^2 + S_z^2} = \gamma \sqrt{S_x'^2 + S_z'^2}$ if the left and right sides are evaluated at the same point in the xz plane.

Regarding the animation, I just want to be clear. For each instant of time, the dipole is at a different location along the y-axis. At each instant, are you plotting the contours as they would exist on a plane perpendicular to the y-axis and located at the instantaneous position of the dipole?

 

[PhDeezNutz]

The animation doesn't look correct to me.

Suppose the primed frame is the frame in which the dipole is at rest. In the unprimed frame, the dipole moves along the y-axis. At the instant the dipole crosses the xz plane in the unprimed system, you can consider the value of the Poynting vector at each point of the xz plane. If you ignore $S_y$ and plot the contour lines of $\sqrt{S_x^2 + S_z^2}$ in the xz plane, I think you will get the same pattern of contours as for a dipole at rest. I find that the only difference is that the value of a particular contour in the xz plane for the moving dipole is greater by the gamma factor $\gamma$ compared to the same contour when the dipole is at rest. In other words, $\sqrt{S_x^2 + S_z^2} = \gamma \sqrt{S_x'^2 + S_z'^2}$ if the left and right sides are evaluated at the same point in the xz plane.

Regarding the animation, I just want to be clear. For each instant of time, the dipole is at a different location along the y-axis. At each instant, are you plotting the contours as they would exist on a plane perpendicular to the y-axis and located at the instantaneous position of the dipole?

A dead give away that my code was wrong was when I set $\beta = 0$ and wasn't able to recover the familiar pattern. I'm an idiot for not considering this.

I am traveling really fast in the y-direction (0.9c) and looking back at the radiation pattern in the xz-plane (with the dipole in the z-direction). Which I'm guessing is equivalent to your description.

I did not ignore $S_y$. Perhaps I should since the entire point of a Poynting vector is to indicate power flux.

edit: for my project I might consider doing a linear accelerated point charge and show how the power profile changes shape.

From pages 7-9 in the document below

http://physics.usask.ca/~hirose/p812/notes/Ch8.pdf

I feel like this can be tied to special relativity because I see betas and gammas everywhere lol.

Edit: It appears that a relativistic accelerating point charge can look like a dipole? I don’t understand that but maybe by the end of the day I will.

 

[PhDeezNutz]

I think one of the mistakes I made was assuming y is still equal to 0 when the frame is traveling.

edit: but maybe that information is already contained within $\vec{\beta} = \beta \hat{y}$ when using the transformation laws on page 558 of Jackson. I’ll keep working on it.

 

[TSny]

I think one of the mistakes I made was assuming y is still equal to 0 when the frame is traveling.

Doing an animation for the moving dipole seems to me to be tricky. But you can get some feeling for the radiation pattern by plotting at just one instant.

I tried plotting contours of S for the yz plane (side view) and the xy plane (overhead view), assuming the dipole moves along the y-axis while the dipole oscillates in the z-direction.

Here's the side view, looking at the yz plane. The dipole moves to the right. The first plot is for the dipole at rest, the middle is for the dipole moving to the right at v = c/3, and the plot on the right is for v = (3/4)c. You can see the Doppler effect where the wavelength is shortened in front of the dipole and stretched out on the backside. The strength of the radiation increases in the forward-moving direction as v increases.

Here's the top view, looking down on the xy plane, for the same selection of speeds. The dipole oscillates in-and-out of the page. The y-axis is still toward the right. Again, you can see the "beaming forward" of the radiation intensity at high speeds.

 

[PhDeezNutz]

You are too helpful. I never even considered doing top and side views. Thank you very much for taking time out of your day (which is clearly not a trivial amount of time) to help me.

hopefully I can generate plots similar to yours.

I will continue to work on it.

Also in earlier post I said something to the effect of me not accounting for position change of the frame...then I realized that the position doesn’t matter but rather the velocity and this dependency is included in $\vec{\beta}$ in Jackson page 558.

 

[PhDeezNutz]

@TSny

I think I got somewhere with it. It seems to look like yours but "flipped". I must have mixed up frame transformations. The picture above is at 0.5c.

To get mine to look more like yours I need to exclude a larger region about the origin to avoid really strong fields. As it is right now I have too many contours close to the origin and the far field just sort of "washes together".

Edit: I used these transformations, it could be that I did them in reverse.

https://wikimedia.org/api/rest_v1/media/math/render/svg/ed275f4351e9a07afd64e9450081851b158c91be

My picture also doesn't seem to be "beaming" so to speak.

 

[TSny]

If you want the dipole to be moving in the +x direction in the primed frame, then the primed frame needs to be moving in the -x direction relative to the unprimed frame.

 

[PhDeezNutz]

If you want the dipole to be moving in the +x direction in the primed frame, then the primed frame needs to be moving in the -x direction relative to the unprimed frame.

I just reversed the sign of v and was able to get something resembling your picture. Minus the "beaming".

I'm about to do something similar for a point charge.

 

[PhDeezNutz]

http://physics.usask.ca/~hirose/p812/notes/Ch8.pdf

May I ask why $\beta = 0$ would result in radiation pattern for a point charge? Bottom of page 8.

 

[TSny]

http://physics.usask.ca/~hirose/p812/notes/Ch8.pdf

May I ask why $\beta = 0$ would result in radiation pattern for a point charge? Bottom of page 8.

I'm not sure I understand your question. A point charge that is instantaneously at rest, but has nonzero acceleration at that instant, will be radiating at that instant.

 

[PhDeezNutz]

I'm not sure I understand your question. A point charge that is instantaneously at rest, but has nonzero acceleration at that instant, will be radiating at that instant.

I think I understand, I mistakingly thought that $\vec{\beta} = 0 \Rightarrow \dot{\vec{\beta}} = 0$ and that's obviously not true. I can't think of an example right now but my assumption is obviously wrong.

 

[PhDeezNutz]

@TSny

Do you know how the fields of a point charge transform under linear acceleration (say in the x-direction)?

I want to reconcile these results with the Lienard-Wiechert results. Do you think that is feasible?

My knowledge of acceleration in special relativity is pretty pathetic. If I recall correctly (I most likely do not) acceleration is directly proportional to velocity in some manner (i.e. damping?).

Also, my professor said that my moving dipole gif was very impressive so I can't thank you enough. He advised that I don't spend any longer time on this project and attend to my other responsibilities because what I've done is more than sufficient...but I'm an addict. I can't miss out on the opportunity to reconcile Lienard-Wiechart results with relativity.

 

[TSny]

@TSny

Do you know how the fields of a point charge transform under linear acceleration (say in the x-direction)?

I want to reconcile these results with the Lienard-Wiechert results. Do you think that is feasible?

I'm not sure I understand the first question above. The fields of an accelerating point charge are typically derived from the Lienard-Wiechert potentials, as in section 8.2 of the link you posted.

My knowledge of acceleration in special relativity is pretty pathetic. If I recall correctly (I most likely do not) acceleration is directly proportional to velocity in some manner (i.e. damping?).

I don't see why $a$ would be proportional to $v$, at least not in general. $a$ can be nonzero at an instant when $v$ is zero.

It seems the discussion is drifting away from the initial topic of this thread. It would probably be best to start another thread if you have general questions regarding the fields of accelerated charges. If the questions are not specific homework questions, then it might be more appropriate to post in the "Classical Physics" forum here or the "Special and General Relativity" forum here

 

[PhDeezNutz]

@TSny I realize that I don't have a very good idea of what I'm talking about and I'm just pontificating at this point.

In the interest of conforming to forum rules/etiquette I shall make a new thread about it when I do have a better idea of what I'm talking about. Don't have long to figure it out lol.

I will update this thread when I've made a 3d dimensional view of the dipole radiation.

Again, thank you for all your help.

 

[PhDeezNutz]

Well I tried to create a 3d animation and I failed pretty bad.

1) The so called "yo-yo" is oriented wrong. I meant for the dipole to be oriented in the z-direction. The lobes should be on the sides instead of the top and bottom. This means I broke up Jackson's expressions wrong component wise.

2) It's not an animation but rather a still picture.

I will continue to work on it. I have to

1) Re-calculate Jackson's expression's component wise so I can re-orient it

2) Find out why my script is not animating. I'll have to look closely at my for loop.

3) Once I find out how to re-orient and animate, I need to learn how to make slices.

Edit: Fixed the orientation but still not animating. The problem was that I was computing the Poynting vector wrong. My image is not as "sharp" was I want it to be...I wonder if that is a limitation on matlab/my computer.

EDIT: nvm I jumped the gun it's not oriented right.

 

[PhDeezNutz]

My picture is right, the middle doesn't fill in because I filtered the zeros in my x,y,z vectors at the beginning. What I need to do is filter just the origin somehow.http://www.antenna-theory.com/antennas/norm3D1lam.jpg

 

[TSny]

What exactly are you plotting in these 3D figures? Are you trying to get the surface that is shown in the link
http://www.antenna-theory.com/antennas/norm3D1lam.jpg ?

 

[PhDeezNutz]

What exactly are you plotting in these 3D figures? Are you trying to get the surface that is shown in the link
http://www.antenna-theory.com/antennas/norm3D1lam.jpg ?

Kind of but not exactly, I should have clarified.

I want to plot level surfaces of the magnitude of the Poynting vector. Basically a 3D version of the gif in post 33. Naturally the outermost level surface will block the view of the rest of the level surfaces.

To me the jpg in the link is a projection of level curves in the xz-plane projected onto a toroid (of sorts).

I believe toroids (of sorts) are the level surfaces of the Poynting vector magnitude but I believe each toroid should be the same color. (I could be wrong)

 

[TSny]

I want to plot level surfaces of the magnitude of the Poynting vector. Basically a 3D version of the gif in post 33. Naturally the outermost level surface will block the view of the rest of the level surfaces.

To me the jpg in the link is a projection of level curves in the xz-plane projected onto a toroid (of sorts).

Yes. The 3D version should just be the 2D version rotated about the z-axis. Below are the 2D and 3D contour graphs I got for one particular value of the magnitude of the Poynting vector. The 3D graph is tilted so that we are looking somewhat down from above.

 

[PhDeezNutz]

Yes. The 3D version should just be the 2D version rotated about the z-axis. Below are the 2D and 3D contour graphs I got for one particular value of the magnitude of the Poynting vector. The 3D graph is tilted so that we are looking somewhat down from above.

View attachment 257366

You are simply amazing. It’s going to be awhile until I have the wherewithal to produce the same graphs as you but I will get there. I’ll work through the night.

Thank you again.

 

[TSny]

You are simply amazing.

No. Mathematica is amazing!

 

[PhDeezNutz]

@TSny I assure you that you are amazing.

Here's an update

My problematic surface arose from me computing Jackson's expressions wrong. Looking at Jackson 9.18.2 I computed $(\vec{n} \times \vec{p}) \times \vec{p}$ instead of the proper $(\vec{n} \times \vec{p}) \times \vec{n}$. I computed the rest of the expression(s) correctly as far as I can tell.

Some comments about my program

1) Still not animating, when it does I need to make coordinate plane slices in a subplot

2) Color scheme washes together; in the far field the variances amongst field strength seem to be so minute that they all become one color. Maybe this is a good thing, maybe it's a bad thing but it is worth mentioning. I'd like to make each shell a different color and somewhat transparent.

 

[PhDeezNutz]

Can anyone think of a clever way to pass a vector of values to a function that only accepts scalars? Using some combination of for loops, while loops, if blocks etc. I want to do it without writing a separate statement for each of the 99 values.

X,Y,Z,

isosurface(X,Y,Z,V,isovalue)

isovalue must be a scalar but like I said I'd like to plot level surfaces for more than just one value without writing a separate statement for each value.

 

[PhDeezNutz]

Not Exactly what I was going for but it is progress.

I have no idea why the shells get intermittently taller (and shorter).

Edit: You would think the shells would change size within an envelope and the envelope itself would not change size.