jeffbarrington
- 23
- 1
Hello,
I'm wondering how you would go about drawing a Feynman diagram for a weak charged current scattering interaction of a positron and a proton. I have attached a diagram of what I have tried but it doesn't conserve lepton number (I think this is a problem, from what I gather non-conservation of lepton number is fringe stuff). It started out with a lepton number of -1 and finishes with +1.
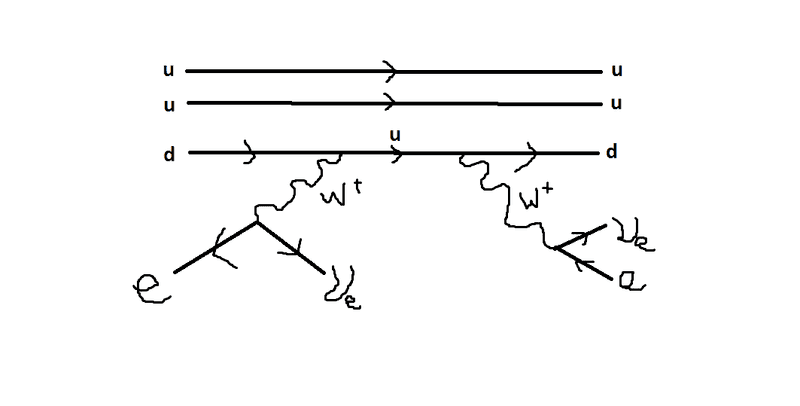
I know it is possible to draw a p/e+ scattering diagram, the question I am looking at asks for one. Would scattering imply that you get e+ and p coming back out, possibly with other particles so long as no conservation laws are violated? Would it still be 'scattering' if one or both of these is missing from the products, say I got a neutron or some mesons coming out instead of a proton?
Thanks
edit - oh I'm dumb the first neutrino given off should be an antineutrino. Never mind. Anyway, is this what you'd draw as a diagram or is there something simpler?
I'm wondering how you would go about drawing a Feynman diagram for a weak charged current scattering interaction of a positron and a proton. I have attached a diagram of what I have tried but it doesn't conserve lepton number (I think this is a problem, from what I gather non-conservation of lepton number is fringe stuff). It started out with a lepton number of -1 and finishes with +1.
I know it is possible to draw a p/e+ scattering diagram, the question I am looking at asks for one. Would scattering imply that you get e+ and p coming back out, possibly with other particles so long as no conservation laws are violated? Would it still be 'scattering' if one or both of these is missing from the products, say I got a neutron or some mesons coming out instead of a proton?
Thanks
edit - oh I'm dumb the first neutrino given off should be an antineutrino. Never mind. Anyway, is this what you'd draw as a diagram or is there something simpler?