- #1
HybridRxN
- 3
- 0
Possible error found in Keith Devlin's book "The Math Gene" Help?
In the section "What is mathematics?" of Keith Devlin's book The Math Gene, he explains to the layman the purpose of abstractions. Devlin uses an example from group theory of symmetry to explain a point. In the example, there's an equilateral triangle with vertices Z,X,and Y from left to right respectively.
This equilateral triangle can be transformed in 6 different ways and still maintain its symmetry.
v = by being rotated 120°
w = by being rotated 240°
I = no change made to equilateral triangle
x = by being reflected on line x, a 90° line*
y = by being reflected on line y, a 330° line*
z = by being reflected on line z, a 210° line*
* I'm referring to angles on a cartesian plane (so where up is 90°, left 180°, down 270°, right 360°/0°)
Devlin then states that you can get to one of the 6 transformations by "combining" two or more of the transformations.
The first equation he writes explaining this concept is x ○ v = y
"G1. For all x,y,z in G, (x * y) * z = x * (y * z)
G2. There is an element e in G such that x * e = e * x = x for all x in G. (e is called an identity element.)
G3. For each element x in G there is an element y in G such that x * y = y * x = e, where e is as in condition G2."
All relevant equations and the copy of the page in the book "Math Gene" can be found here:
http://bit.ly/13pzUHa
Start with the paragraph that states "Consider, for example, a symmetry group..." on pg.108 and continue to pg.109
The problem is that this equation doesn't make since to me after I checked it with the operations. I don't know if Devlin made a typo or if I'm doing something wrong.
So I start with the equilateral triangle (z, x, y).
Then I perform the 'x' transformation (reflection on line x) which switches the y and z getting (y, x, z)
Then I perform the 'v' transformation (120° rotation) which moves the vertices down one getting (z, y, x).
Lastly I check to see if this equals a 'y' transformation (reflection on line y) of the equilateral triangle which is (x, z, y).
Well clearly (x,z,y) and (z,y,x) don't match up, so either I'm doing it wrong or he made a typo.
Just to make sure I was doing the right thing I tried a different equation.
x ○ y = v
I take the equilateral triangle (z,x,y)
I apply a x transformation (reflection on line x) (y,x,z)
Next I apply a y transformation (reflection on line y) to the preceding transformation (y,z,x)
I check to see if this matches a v transformation (rotating triangle 120°) (y,z,x)
and it does.
Here's a picture showing my work and the manipulations.
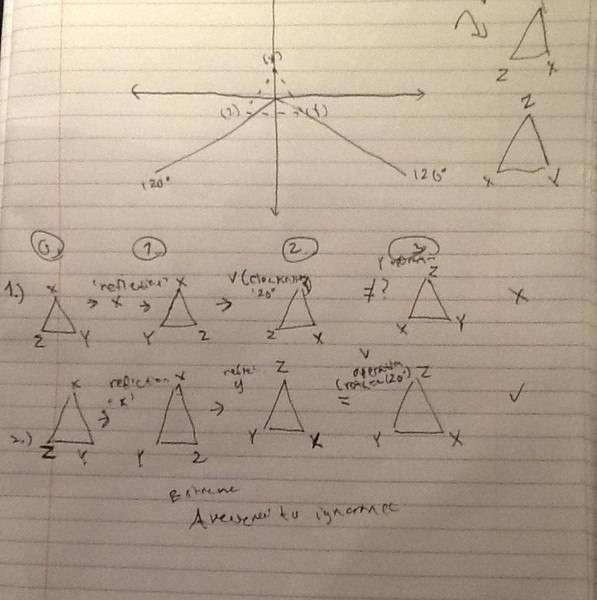
So now I'm confused. I'm trying to follow along with him logically, but I don't understand what happened here. (Maybe incorrect interpretation of the symbol '○' ?) If this is a mistake on his part, I'll begin to lose his respect. It could possibly be an error of my own. In any case I'm trying to LEARN.
So does someone mind checking the validity of aforementioned equation?
BTW: As for my math background, I'm a high school senior and I'm working (struggling...) through AP Calc BC this year--good grasp of the concepts, poor arithmetic skills :P I blame my crappy Pre-Cal teacher.
Homework Statement
In the section "What is mathematics?" of Keith Devlin's book The Math Gene, he explains to the layman the purpose of abstractions. Devlin uses an example from group theory of symmetry to explain a point. In the example, there's an equilateral triangle with vertices Z,X,and Y from left to right respectively.
This equilateral triangle can be transformed in 6 different ways and still maintain its symmetry.
v = by being rotated 120°
w = by being rotated 240°
I = no change made to equilateral triangle
x = by being reflected on line x, a 90° line*
y = by being reflected on line y, a 330° line*
z = by being reflected on line z, a 210° line*
* I'm referring to angles on a cartesian plane (so where up is 90°, left 180°, down 270°, right 360°/0°)
Devlin then states that you can get to one of the 6 transformations by "combining" two or more of the transformations.
The first equation he writes explaining this concept is x ○ v = y
Homework Equations
"G1. For all x,y,z in G, (x * y) * z = x * (y * z)
G2. There is an element e in G such that x * e = e * x = x for all x in G. (e is called an identity element.)
G3. For each element x in G there is an element y in G such that x * y = y * x = e, where e is as in condition G2."
All relevant equations and the copy of the page in the book "Math Gene" can be found here:
http://bit.ly/13pzUHa
Start with the paragraph that states "Consider, for example, a symmetry group..." on pg.108 and continue to pg.109
The Attempt at a Solution
The problem is that this equation doesn't make since to me after I checked it with the operations. I don't know if Devlin made a typo or if I'm doing something wrong.
So I start with the equilateral triangle (z, x, y).
Then I perform the 'x' transformation (reflection on line x) which switches the y and z getting (y, x, z)
Then I perform the 'v' transformation (120° rotation) which moves the vertices down one getting (z, y, x).
Lastly I check to see if this equals a 'y' transformation (reflection on line y) of the equilateral triangle which is (x, z, y).
Well clearly (x,z,y) and (z,y,x) don't match up, so either I'm doing it wrong or he made a typo.
Just to make sure I was doing the right thing I tried a different equation.
x ○ y = v
I take the equilateral triangle (z,x,y)
I apply a x transformation (reflection on line x) (y,x,z)
Next I apply a y transformation (reflection on line y) to the preceding transformation (y,z,x)
I check to see if this matches a v transformation (rotating triangle 120°) (y,z,x)
and it does.
Here's a picture showing my work and the manipulations.
So now I'm confused. I'm trying to follow along with him logically, but I don't understand what happened here. (Maybe incorrect interpretation of the symbol '○' ?) If this is a mistake on his part, I'll begin to lose his respect. It could possibly be an error of my own. In any case I'm trying to LEARN.
So does someone mind checking the validity of aforementioned equation?
BTW: As for my math background, I'm a high school senior and I'm working (struggling...) through AP Calc BC this year--good grasp of the concepts, poor arithmetic skills :P I blame my crappy Pre-Cal teacher.