rayhan619
- 75
- 0
Homework Statement
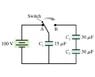
Initially, the switch in the figure is in position A and capacitors C_2 and C_3 are uncharged. Then the switch is flipped to position B. (Figure attached)
a) Afterward, what is the charge on C_1 capacitor?
b) Afterward, what is the potential difference across C_1 capacitor?
c) Afterward, what is the charge on C_2 capacitor?
d) Afterward, what is the potential difference across C_2 capacitor?
e) Afterward, what is the charge on C_3 capacitor?
f) Afterward, what is the potential difference across C_3 capacitor?
Homework Equations
V= IR
The Attempt at a Solution
How do I start this problem?