Potential Energy and Conservation Of Energy Atwood's Machine

[godkills]

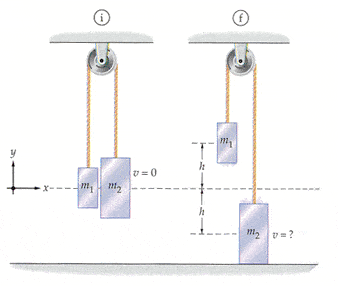
The two masses in the Atwood's machine shown in Figure 8-23 areinitially at rest at the same height. After they are released, thelarge mass, m2, falls through a heighth and hits the floor, and the small mass,m1, rises through a height h.


(a) Find the speed of the masses just beforem2 lands. Assume the ropes and pulley have negligible massand that friction can be ignored. (Use m1 form1, m2 for m2, andh and g as necessary.)

(b) Evaluate your answer to part (a) for the case where h= 1.2 m, m1 =3.7 kg, and m2 =4.1 kg.

So what I basically did was state the fact that E_i= E_f

Initial Potential Energy U_i = m₁gh + m₂gh
Initial Kinetic Energy would be 0 for both masses due to the masses at rest.

Final Potential Energy U_f = m₁gh + 0 (due to the object being at rest on floor)
Final Kinetic Energy = .5v²(m₁ + m₂)

E_i= E_f

m₁gh cancels out for both sides.
Leaving this (4.1)(9.81)(1.2) = 5v²(3.7+4.1)

Velocity is 3.52 m/s

Anyone have any idea if answer is correct? I am currently unsure if i did it correctly but i compared it to this procedure.

http://tinyurl.com/4xcrvea"

If the link above shows correct procedure can somebody explain why the potential energy of final is 2h? Also somehow the algebra doesn't make sense where the person managed to get (m2-m1) someone care to explain this? This kind of makes me furious on how I am not able to understand how the person did this!

 

[Cameron Knight]

This isn't correct. I haven't analyzed your process but it follows the basic form that the energy is conserved. This special case, however, in the final stage, the height of the first mass is doubled, so potential energy has increased instead of going to zero as it did for the second mass. KEf = 1/2m(1)v^2+1/2m(2)v^2+m(1)g(2)h

 

[Doc Al]

If the link above shows correct procedure can somebody explain why the potential energy of final is 2h?

m₁ rises from the initial height of h to a final height of 2h, so the final PE (using the given reference level) is 2m₁gh. (You forgot the change in PE of m₁.)