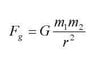What Is the Potential Energy and Gravitational Force on a Satellite?

AI Thread Summary
The discussion focuses on calculating the potential energy and gravitational force on a satellite orbiting Earth at an altitude of 2.00x10^6m. The potential energy is determined using the formula Ug = -G m1m2/r, where G is the universal gravitational constant. The mass of the Earth is provided as 5.98x10^24 kg, and the radius of Earth is 6.37x10^6 m. For the gravitational force, participants suggest using Newton's equation for gravitational force, which also incorporates the gravitational constant G. The conversation highlights the importance of correctly identifying the equations needed for these calculations.
Husker70
Messages
89
Reaction score
0

Homework Statement


A satellite of the Earth has a mass of 100kg and is at an altitude of 2.00x10^6m.
(a) What is the potential energy of the satellite-Earth system? (b) What is the magnitude
of the gravitational force exerted by the Earth on the satellite? (c) What force does the
satellite exert on the Earth?


Homework Equations


(a) Ug = - G m1m2/r
Mass of Earth = 5.98x10^24 kg
Radius of Earth = 6.37x10^6 m

The Attempt at a Solution


(a) I took the mass of the Earth times the 100kg satellite/the Altitude plus the radius of earth
Ug = G (5.98x10^24kg)(100kg)/2.00x10^6m(6.37x10^6m)
I'm not sure what the G is for.
Thanks,
Kevin
 
Physics news on Phys.org
G is the universal gravitational constant:

G=6.67*10^{-11}\frac{Nm^2}{kg^2}
 
Got it thanks. Not sure why I couldn't find that but I got the correct answer.
Not sure what equation to use for part b
Thanks,
Kevin
 
For part b), you want Newton's equation for the force of gravity between two objects:

HINT: The equation your looking for should also contain a big G.
 
I think I got it using this equation.
Thanks,
Kevin
 

Attachments

  • ForceGravity.jpg
    ForceGravity.jpg
    1.7 KB · Views: 614

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

When do I include the Earth's radius in questions involving satellites?
Replies
5
Views
2K
Gravitational potential energy traveling from earth to mars
Replies
7
Views
3K
Potential Energy and raising a satellite from Earth into a Circular Orbit
Replies
5
Views
2K
Gravitational potential energy, orbital speed, binding energy.
Replies
3
Views
3K
Acceleration of object at specific height?
Replies
8
Views
2K
Where between the Moon and the Earth is the gravitational potential=0 ?
Replies
21
Views
3K
How much work is done when a satellite is launched into orbit?
Replies
5
Views
2K
Energy of Satellites(Homework question)
Replies
1
Views
1K
The Height and Speed of a Geosynchronous Satellite
Replies
11
Views
2K
Conservation of Energy with Gravitational Potential Energy
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top