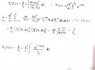Potential of a hydrogenic ion given a wavefunction

[Manuel Galdon]

EDIT: moved from technical forum, so no template

Hello, I have a problen which is about calculating an electrostatic potential for a hydrogenic atom in the ground state given its wavefunction. Since I know the wavefunction of the ground state I would find it by solving the Schrödinger equation, but the statement gives us an expression to calculate it.

This is all what the problem says. Any ideas? Just put the wavefunction into the integral and go on ?

Thanks !

 

[Dale]

Hi Manuel, welcome to PF!

Can you show some of your work so far?

 

[Manuel Galdon]

Hi Manuel, welcome to PF!

Can you show some of your work so far?

For now I only have the multipolar expansion for l=0.

What do the indexes in the spherical harmonics stand for? Should I understand that the hydrogenic ion is an hydogen atom with 2 electrons and therefore the indexes in the spherical harmonics concern the electrons 1 and 2? I think I have never worked with such system, I am a little lost with the notation and, as you can see, the problem statement does not tell too much.

 

[Dale]

What do the indexes in the spherical harmonics stand for? Should I understand that the hydrogenic ion is an hydogen atom with 2 electrons and therefore the indexes in the spherical harmonics concern the electrons 1 and

A hydrogenic (or hydrogen-like) ion is an ion with only 1 electron. So for example He+.

 

[Manuel Galdon]

So I should understand the problem as an atom with only one electron, right? Finally I got this expression $$\int\frac{1}{r_> e^{2zr_1}} dr_1$$
If the electron is in the position r1 and we supose that r0>r1 , then have $$\int\frac{1}{r_0 e^{2zr_1}} dr_1 = \frac{1}{r_0}\int\frac{1}{e^{2zr_1}} dr=-\frac{e^{-2zr_0}}{2z}$$

Do you agree? This is the electrostatic potential evaluated in r0. I guess this is the point where we have to evaluate it because the problem gives the formula for the potential evaluated in such point.

 

[blue_leaf77]

How did you get this

$$\int\frac{1}{r_> e^{2zr_1}} dr_1$$

?
In order to evaluate such an integral you have there, you can divide the integration range into two:
$$
\int_0^{r_0} \int_0^{\pi} \int_0^{2\pi} \frac{|\psi(r_1)|^2}{r_{01}} r_1^2 \sin\theta_1 dr_1 d\theta_1 d\phi_1 + \int_{r_0}^\infty \int_0^{\pi} \int_0^{2\pi} \frac{|\psi(r_1)|^2}{r_{01}} r_1^2 \sin\theta_1 dr_1 d\theta_1 d\phi_1
$$
In the first integral, $r_1 < r_0$, and in the second one $r_1 < r_0$. From this you can substitute the correct form of the expansion of $1/r_{01}$ given there.

 

[Manuel Galdon]

I evaluated the integral without taking the limits into consideration and I only evaluated the radial part. How do you know about the angular parts involved here?

Regarding the expansion of r01, I used the expansion for l=0 since the atom is in the ground state. Do you agree?

 

[blue_leaf77]

How do you know about the angular parts involved here?

The angular part must be involved because you are calculating a volume integral. $d\mathbf{r}_1$ is a volume element, and it is equal to $r_1^2 \sin\theta_1 dr_1 d\theta_1 d\phi_1$.

Regarding the expansion of r01, I used the expansion for l=0 since the atom is in the ground state. Do you agree?

That series will indeed shrink down to one term corresponding to $Y_{00}$ but you have got to have an authentic reason to justify your reasoning.

we supose that r0>r1

That's not how you should proceed to answer a physics problem. If there is still more reliable way to do things, you have to follow this path.
Now, just try plugging in the expansion of $1/r_{01}$ into the first integral I wrote in post #6.