jaus tail
- 613
- 48
Homework Statement
Homework Equations
I rms for triangular waveform = I(max)/ (1.732)
R = V/I
The Attempt at a Solution
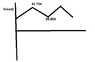
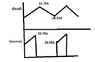
Since there is RLE load, current waveform is triangular. It is
Source current is
Average of I source. I used integration. Assumed Time period = 10 seconds. So T on = 5 seconds. (question says duty = 0.5)
So integrating I got average source current = 14.7 A
Average source voltage = 200 V
So input resistance = 200 / 14.7 = 13.6A
But I'm not able to get the first one. I get answer as 26.33 A But that is not even in the option.
I used formula square I(load) = square dc component (26.05) + square (rms of triangular waveform)
Attachments
Last edited:


 The homework would not expect you to, the triangular approximation is fine. Though in the real world you should show that the triangular approximation is justified and not simply assume it is, i.e., not just hope it is.
The homework would not expect you to, the triangular approximation is fine. Though in the real world you should show that the triangular approximation is justified and not simply assume it is, i.e., not just hope it is.
