athrun200
- 275
- 0
Can Power supply be smaller than power dissipated?
Because I saw this in one question
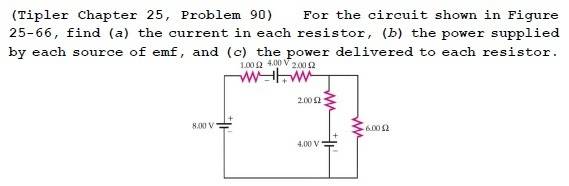

There are 3 cells, the power supply of the two 4V cells cancel each other. (one is -4W and another one is 4W)
So the total power supply should be 16W
But in part c, the power dissipated is 4+8+2+6=20W
Power supply < power dissipated?
Because I saw this in one question
There are 3 cells, the power supply of the two 4V cells cancel each other. (one is -4W and another one is 4W)
So the total power supply should be 16W
But in part c, the power dissipated is 4+8+2+6=20W
Power supply < power dissipated?