Kalus
- 36
- 0
Ok, this is a very basic question, but for some reason my head can't work out the last bit and its making me doubt the workings...
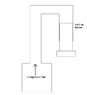
As the attached diagram shows, there is an air compressor attached to a piece of metal pipe that then has a piston on the end. The goal is to make this piston produce 200N of force. It has a radius of 25mm or 0.025 m, meaning an area of 1.96 x10^-3 m^2.
This means that if you use pressure= force/ area
pressure = 200/1.96 x10^-3
=101,859 Pa
This is almost equivilant to 1bar, which is around 14.5 PSI.
Does this mean that to produce that force i need to have a compressor that will pump air to just over one atmosphere?
This is the bit that confuses me, because surely air is at atmospheric pressure already, so it should be exerting that pressure if i just didnt have a compressor at all and left the tube pointing up open topped?
So, is that calculation correct, and if so, what am i not understanding about the way atmospheric pressure works?
Many Thanks, Kalus.
As the attached diagram shows, there is an air compressor attached to a piece of metal pipe that then has a piston on the end. The goal is to make this piston produce 200N of force. It has a radius of 25mm or 0.025 m, meaning an area of 1.96 x10^-3 m^2.
This means that if you use pressure= force/ area
pressure = 200/1.96 x10^-3
=101,859 Pa
This is almost equivilant to 1bar, which is around 14.5 PSI.
Does this mean that to produce that force i need to have a compressor that will pump air to just over one atmosphere?
This is the bit that confuses me, because surely air is at atmospheric pressure already, so it should be exerting that pressure if i just didnt have a compressor at all and left the tube pointing up open topped?
So, is that calculation correct, and if so, what am i not understanding about the way atmospheric pressure works?
Many Thanks, Kalus.