Darcy30
- 1
- 1
Hallo. Since I'm new in this field, I hope someone can help me.
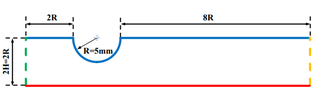
I have a laminar, steady state, incompressible flow in a channel (a fully developed).
Geometry of the channel is on the photo.
How should I calculate the drop of static pressure across the channel?
Since I have Re, I did calculate a inlet velocity, but now I'm stuck.
Thanks
I have a laminar, steady state, incompressible flow in a channel (a fully developed).
Geometry of the channel is on the photo.
How should I calculate the drop of static pressure across the channel?
Since I have Re, I did calculate a inlet velocity, but now I'm stuck.
Thanks