Pressure in piezometers with ideal fluid

[fog37]

Hello,
I am trying to understand how to apply Bernoulli's equation (which is valid along a single streamline and in the case of zero viscosity) to the situation below.

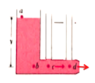
The ideal fluid moves at constant speed along the horizontal pipe. Because the fluid is ideal (zero viscosity), the ideal fluid will reach zero height inside any of the vertical piezometers. Why? I know there is no pressure drop along the horizontal pipe since the viscosity is zero.

If the viscosity was not zero, the fluid would actually reach a nonzero height along the first piezometer and a lower, nonzero height in the second piezometer (to indicate the pressure drop). How come the viscous fluid would manage to go up the piezometric tubes while the ideal fluid does not?

Thanks.

 

[Chestermiller]

For an inviscid fluid, the pressure at the exit of the tank is equal to atmospheric pressure, so there is no pressure variation along the horizontal pipe. The pressure at the base of each piezometer is atmospheric, so the fluid cannot rise.

If the fluid is viscous, then there is a pressure drop from the inlet end to the exit end of the horizontal pipe, and the pressure varies linearly from the inlet end to the outlet end. This means that the pressure at the exit of the tank is higher than atmospheric pressure. The pressure has to be higher than atmospheric at the tank exit to overcome the viscous drag in the horizontal pipe.

 

[fog37]

Thanks Chestermiller,

So, in the case of an ideal inviscid fluid, we have the following pressures:

The fluid must accelerate between point 1 (pressure higher than atmospheric pressure) and point 2 (atmospheric pressure). After that, the fluid proceeds at constant speed (continuity equation). There must therefore be a pressure gradient from point 1 to point 2. Does the pressure become atmospheric even before point 2 along the pipe?

Why would the pressure at points 2,3,4 be atmospheric and not equal $(P_{atm}+\rho g h_{0})$, i.e. the same pressure value as in point 1? I understand that on the right side of the exit orifice of the horizontal pipe the water stream is free and is the open atmosphere so the pressure on it is atmospheric. But to the right of the orifice, the pressure should not be atmospheric pressure. Why is it? If we cut the horizontal pipe (i.e. perform the Torricelli experiment), the pressure at the drain is always taken as atmospheric if the drain hole is very small and we are considering a point just outside the hole, in the open atmosphere.

In some textbooks we see an ideal non viscous fluid flowing in a pipe and the piezometers along the pipe have fluid reaching the same height (to indicate no loss in pressure) but those heights are not zero, like in the figure below (point c and d):

What am I missing? I know that Bernoulli's equation needs to be applied to a single streamline, inside an ideal fluid and that the sum of the three heights (geodetic, piezometric and kinetic) must be constant.

 

[Chestermiller]

In the first figure, the pressure at point 1 is not given by the hydrostatic equation, even for an inviscid fluid. Within the tank, in the region approaching the exit hole, the flow is accelerating toward the hole and the pressure is decreasing. The effective region where this occurs is within a few hole diameters of the exit hole. So the pressure at the exit hole is atmospheric, not hydrostatic.

In the 2nd figure, there are decreases in cross sectional area in the horizontal tube, so, by Bernoulli's equation, the pressures at e and f are higher than atmospheric, and the pressures at b and c are higher than at e and f.

 

[fog37]

Ok, great, thanks! I am making some progress.

So, just to make sure, still talking about the ideal inviscid fluid, if we cut the horizontal pipe to exclude the section with the constriction (where pressure is reduced) the fluid height in the two piezometric tubes at point c and d would go down to zero and would NOT look like

but like

However, if the fluid was viscous, the figure would look like

At the exit hole, the pressure is still atmospheric. The pressure $P_b > P_c> P_d >P_{atm}$. The fact that a the liquid can climb up the piezometers in the case of a viscous fluid is due to the fact that the pressure gradient exist along the entire horizontal pipe and the pressure differences are manifested as nonzero heights along the piezometers...

 

[Chestermiller]

Ok, great, thanks! I am making some progress.

So, just to make sure, still talking about the ideal inviscid fluid, if we cut the horizontal pipe to exclude the section with the constriction (where pressure is reduced) the fluid height in the two piezometric tubes at point c and d would go down to zero and would NOT look like
View attachment 110353

but like

View attachment 110354

However, if the fluid was viscous, the figure would look like

View attachment 110355

At the exit hole, the pressure is still atmospheric. The pressure $P_b > P_c> P_d >P_{atm}$. The fact that a the liquid can climb up the piezometers in the case of a viscous fluid is due to the fact that the pressure gradient exist along the entire horizontal pipe and the pressure differences are manifested as nonzero heights along the piezometers...

Yes. Perfect, except that the pressures at the base of the vertical tubes (not the pressure differences) are manifested as nonzero heights along the pizometers.

 

[fog37]

Great!
I am quite satisfied with this minor achievement and relieved to know that, in the case of an inviscid fluid, the two figures are not incompatible with each other and both correct:

(no restrictions or expansions in the horizontal pipe).What threw me off was the nonzero height reached by the inviscid fluid in the first figure and the zero height in the 2nd figure. The difference is due to the different container configurations.

If we closed the exit hole in the horizontal pipe the fluid would soon reach the same height in all the piezometric tubes in both configurations. Of course, the longer the horizontal tube the lower the height reached by the fluid will be in that static situation (communicating vessels principle).

 

[fog37]

I am re-reading the content of this thread on piezometric measurements and realized that I still have some doubts. Let me explain and hope you can help:

CASE 1: The figure below illustrates what happens in the case of an inviscid (zero viscosity) fluid flowing inside a horizontal constant cross-section pipe connected to the bottom of a container. No fluid would rise inside the two vertical piezometers which implies zero gauge pressure: the pressure at points $c$ and $d$ inside the fluid is equal to $P_{atm}$. I am confident in this result.

The next figure shows instead what would happen if the fluid had nonzero viscosity.

• What would the gauge pressure $P_b$be in that case? Would it be close but smaller than the hydrostatic pressure at that depth?
• What would the gauge pressure $P_c$ be in that case? What determines its magnitude? Does the distance of point $c$ from point $b$ determine its magnitude?

I believe this third figure below represents an impossible case: the gauge pressure is nonzero and identical in both vertical piezometers and the pipe cross-section is constant. Would that be possible?

CASE 2: The figure below still deals with an inviscid fluid (I believe) flowing inside a non-constant cross-section pipe. I think the fluid is inviscid because the pressure at point $c$ and $d$ remains the same in the constant cross-section segment: $P_{c}$ = $P_{d}$. The same goes for $P_{e}$ = $P_{f}$. However the pressure $P_{d}$ > $P_{e}$ just because of the pipe constriction and not because of a pressure drop due to nonzero viscosity. As mentioned, the liquid is inviscid.

• So why is the gauge pressure in the piezometers not zero, i.e. $P_{c}$ = $P_{d}= P_{atm}$, like it happens in case 1 if the fluid is truly inviscid?
• What physically causes the fluid to rise in the tubes above point $c$ and $d$?
• What is the approximate gauge pressure at point $c$?

Thanks for your help!

 

[Chestermiller]

I am re-reading the content of this thread on piezometric measurements and realized that I still have some doubts. Let me explain and hope you can help:

CASE 1: The figure below illustrates what happens in the case of an inviscid (zero viscosity) fluid flowing inside a horizontal constant cross-section pipe connected to the bottom of a container. No fluid would rise inside the two vertical piezometers which implies zero gauge pressure: the pressure at points $c$ and $d$ inside the fluid is equal to $P_{atm}$. I am confident in this result.

Some of the figures for Case 1 show the duct converging just before the exit to the atmosphere, and some show a negligible amount of this. I'm going to assume that they all don't include converging section before the exit.

View attachment 216771
The next figure shows instead what would happen if the fluid had nonzero viscosity.

• What would the gauge pressure $P_b$be in that case? Would it be close but smaller than the hydrostatic pressure at that depth?

As the entrance to the lower duct is approached, the pressure at point b is getting closer to the total viscous pressure drop in the entire tube, and less close to hydrostatic.

• What would the gauge pressure $P_c$ be in that case? What determines its magnitude? Does the distance of point $c$ from point $b$ determine its magnitude?

The gauge pressure at point C would depend on the viscous pressure drop between point C and the tube exit. This depends on many factors including the volumetric rate of flow, tube diameter, fluid density, fluid viscosity, and distance to the exit. Of course, it can't be higher than the hydrostatic pressure in the tank.

The line you have drawn should pass through zero rise at the tube exit. Typically, I would expect the slanted line in the figure to be lower.

View attachment 216776

I believe this third figure below represents an impossible case: the gauge pressure is nonzero and identical in both vertical piezometers and the pipe cross-section is constant. Would that be possible?
View attachment 216777

It applies neither to viscous flow nor inviscid flow

CASE 2: The figure below still deals with an inviscid fluid (I believe) flowing inside a non-constant cross-section pipe. I think the fluid is inviscid because the pressure at point $c$ and $d$ remains the same in the constant cross-section segment: $P_{c}$ = $P_{d}$. The same goes for $P_{e}$ = $P_{f}$. However the pressure $P_{d}$ > $P_{e}$ just because of the pipe constriction and not because of a pressure drop due to nonzero viscosity. As mentioned, the liquid is inviscid.

• So why is the gauge pressure in the piezometers not zero, i.e. $P_{c}$ = $P_{d}= P_{atm}$, like it happens in case 1 if the fluid is truly inviscid?

The fluid has to be accelerated in the converging sections between the constant-diameter sections. This requires a higher upstream pressure than downstream pressure.

• What physically causes the fluid to rise in the tubes above point $c$ and $d$?

The pressures at c and d are above atmospheric, and the pressure at the top of these columns is atmospheric. So, in order for a vertical force balance to exist, a column of liquid has to be present. This is all just hydrostatic.

• What is the approximate gauge pressure at point $c$?

I think that you personally should be able to work this out using the Bernoulli equation. Let's see your attempt.

View attachment 216774

 

[fog37]

Well, I think the pressure $P_b ~ \rho g y$. Since the efflux speed is $\sqrt{2 g y}$, Bernoulli equation would give that the pressure at point $c$ is $$P_c= \rho g y - \frac {\rho } {2} (2g y) $$

Also, for those interested in this topic (like me), I found these figures showing the impact that the orifice size and shape can have on the ideal efflux speed $\sqrt{2 g y}$. I wasn't aware of that.

I notice from the figure (a) above that there are multiple streamlines reaching the bottom orifice. We can only apply Bernoulli principle to a single streamline. Does it matter which one we choose?

 

[Chestermiller]

Well, I think the pressure $P_b ~ \rho g y$. Since the efflux speed is $\sqrt{2 g y}$,

This is incorrect. Depending on the exact location you specify for point b, the pressure will be somewhere between $\rho g y$ and something somewhat less than this. You can see this from the other figures you have provided, where the streamlines are converging toward the orifice. So, as the streamlines converge, the velocity for the fluid between pairs of streamlines increases (to preserve the volumetric throughput rate). This increase in flow velocity is accompanied by a decrease in pressure. So, in regions where the streamlines are far apart, the pressure will approach $\rho g y$, but at the orifice, the pressure will be lower. Note that all the pressure variations we are describing here occur within the tank in the region approaching the orifice.

Bernoulli equation would give that the pressure at point $c$ is $$P_c= \rho g y - \frac {\rho } {2} (2g y) $$

This is incorrect too. If $A_c$ is the cross sectional area at c and $A_h$ is the cross sectional area at h, the velocity at c is related to the velocity at h by: $$v_c=\frac{A_h}{A_c}v_h$$So, applying Bernoulli's equation gives:
$$p_c+\frac{\rho}{2}\left(\frac{A_h}{A_c}\right)^2v_h^2=\frac{\rho}{2}v_h^2$$
or
$$p_c=\rho g y\left[1-\left(\frac{A_h}{A_c}\right)^2\right]$$

 

[fog37]

I see. Thank you.

My mistake was assuming that the speed at point $b$ was about zero and speed at $c$ was the same as the efflux speed $\sqrt{2g y}$ and applied Bernoulli's equations between two two points...

 

[fog37]

Chestermiller, thanks again.

I understand the meaning of the continuity equation: it assures flow rate continuity (assuming constant density and incompressible fluid) and tells us that the fluid pressure decreases while the speed increases when the fluid goes through a pipe constriction of smaller cross-section.

The term $p$ in Bernoulli's equation, I believe, indicates the "static" pressure. We often read that the total pressure is $$P_{tot} = P_{dynamic} + P_{static}$$ as if there were two types of pressure, "static" and "dynamic". This distinction is artificial since there is only one pressure, physically interpreted as the average compressive force per unit area exerted by the fluid molecules. The total pressure $P_{tot}$ would be measured by a test area oriented perpendicular to the flow (like test areas $A_a$ and $A_d$) to include the momentum deriving from the fluid being into motion. Test areas $A_b$, instead, would only measure hydrostatic pressure, and test area $A_c$ would measure a pressure between $P_{total}$ and $P_{static}$, correct?

The "static" pressure is the isotropic pressure contribution to the total that exists no matter how we would orient a test area inside a flowing or static fluid, correct?

Back to Bernoulli's equation $$P + \frac{1}{2} \rho v^2+ \rho g y= constant$$, the entire trinomial should actually represent the total pressure $P_{total}$ since it is the sum of the term $P_{static} = p_{atmospheric} + \rho g y$ and the dynamic pressure term $P_{dynamic} = \frac{1}{2} \rho v^2$.

So, when we say that the measured fluid pressure in a pipe constriction is lower, are we referring to the total pressure since the static pressure would not change (assuming same elevation)? However, we use piezometers (and notice that the fluid height is lower in the piezometer in the constriction). But a piezometer measures static gauge pressure since the area under the piezometer is like area $A_b$, i.e. parallel to the flow and seems to not be "sensitive" to the kinetic contribution of the fluid flow...

 

[Chestermiller]

Chestermiller, thanks again.

I understand the meaning of the continuity equation: it assures flow rate continuity (assuming constant density and incompressible fluid) and tells us that the fluid pressure decreases while the speed increases when the fluid goes through a pipe constriction of smaller cross-section.

All the continuity equation tells us is that the velocity at c times the cross sectional area at c is equal to the velocity at f times the cross sectional area at f. To reach the conclusion that the pressure decreases while the speed increases, we need to combine this with the Bernoulli equation.

The term $p$ in Bernoulli's equation, I believe, indicates the "static" pressure. We often read that the total pressure is $$P_{tot} = P_{dynamic} + P_{static}$$ as if there were two types of pressure, "static" and "dynamic". This distinction is artificial since there is only one pressure, physically interpreted as the average compressive force per unit area exerted by the fluid molecules. The total pressure $P_{tot}$ would be measured by a test area oriented perpendicular to the flow (like test areas $A_a$ and $A_d$) to include the momentum deriving from the fluid being into motion. Test areas $A_b$, instead, would only measure hydrostatic pressure, and test area $A_c$ would measure a pressure between $P_{total}$ and $P_{static}$, correct?

The "static" pressure is the isotropic pressure contribution to the total that exists no matter how we would orient a test area inside a flowing or static fluid, correct?

As a guy with lots of experience in fluid mechanics, I have no value for the concepts of dynamic pressure and total pressure since, in my judgment, they only serve to confuse the student (as they have done for you). The entity you call the "static pressure" is what I would refer to as the plain old "pressure."

Back to Bernoulli's equation $$P + \frac{1}{2} \rho v^2+ \rho g y= constant$$, the entire trinomial should actually represent the total pressure $P_{total}$ since it is the sum of the term $P_{static} = p_{atmospheric} + \rho g y$ and the dynamic pressure term $P_{dynamic} = \frac{1}{2} \rho v^2$.

So, when we say that the measured fluid pressure in a pipe constriction is lower, are we referring to the total pressure

No. We are referring to the static pressure.

since the static pressure would not change (assuming same elevation)?

You seem to be confusing the term static pressure with the term "hydrostatic pressure."

However, we use piezometers (and notice that the fluid height is lower in the piezometer in the constriction). But a piezometer measures static gauge pressure since the area under the piezometer is like area $A_b$, i.e. parallel to the flow and seems to not be "sensitive" to the kinetic contribution of the fluid flow...

View attachment 216844

See what I mean when I say that using terminology like "dynamic pressure" and "total pressure" causes confusion for students. My advice is to purge them from your vocabulary.

 

[fog37]

Hi Chestermiller,
Thank you again. I am indeed confused on the difference between "hydrostatic" pressure (which I think I understand well) and static pressure in the context of moving fluids. What is the exact difference?

Hydrostatic pressure: it is the isotropic pressure measured in a fluid at rest. The small liquid molecules, on average cause a pressure on a test area located in the fluid and the pressure is the same no matter the test area orientation. This pressure $P_{hydrostatic} = \rho g y + P_{atmos}$ linearly depends on depth and on the fluid density (we also add the atmospheric pressure contribution acting on the fluid free surface).

Static pressure in a moving fluid: I read an explanation about static pressure from Kim Aaron's response on Quora but that explanation seems very similar to how hydrostatic pressure works. I understand that, if the fluid parcel accelerates and changes speed as it passes into a pipe constriction, a pressure gradient large pressure followed by a smaller pressure in the constriction must exist to create a force that accelerates the fluid particle itself. But that static pressure seems quite similar in nature to hydrostatic pressure as it appears to also be isotropic and it is measured as a gauge pressure using a vertical piezometer tube, the sam way hydrostatic pressure is measured.

Thanks,
Fog37

 

[Chestermiller]

Hi Chestermiller,
Thank you again. I am indeed confused on the difference between "hydrostatic" pressure (which I think I understand well) and static pressure in the context of moving fluids. What is the exact difference?

Hydrostatic pressure: it is the isotropic pressure measured in a fluid at rest. The small liquid molecules, on average cause a pressure on a test area located in the fluid and the pressure is the same no matter the test area orientation. This pressure $P_{hydrostatic} = \rho g y + P_{atmos}$ linearly depends on depth and on the fluid density (we also add the atmospheric pressure contribution acting on the fluid free surface).

Static pressure in a moving fluid: I read an explanation about static pressure from Kim Aaron's response on Quora but that explanation seems very similar to how hydrostatic pressure works. I understand that, if the fluid parcel accelerates and changes speed as it passes into a pipe constriction, a pressure gradient large pressure followed by a smaller pressure in the constriction must exist to create a force that accelerates the fluid particle itself. But that static pressure seems quite similar in nature to hydrostatic pressure as it appears to also be isotropic and it is measured as a gauge pressure using a vertical piezometer tube, the sam way hydrostatic pressure is measured.

Thanks,
Fog37

Static pressure, or, as I call it, plain old pressure: Is it possible to have static pressure in a horizontal system (where no elevation is involved and no connection to the atmosphere is involved)?

 

[fog37]

Well, I am not sure. All I know is that "static" pressure is also known as thermodynamic pressure.

I can see how a moving fluid impacting on a surface exerts a larger pressure than if the fluid was at rest. And if the impact area is parallel to the flow, the fluid molecules' should produce the same pressure that is produced when the fluid is not moving since the fluid molecule's momentum has not component perpendicular to the area surface...That is why I am led to believe that hydrostatic and "static" pressure should be the same...

 

[Chestermiller]

Well, I am not sure. All I know is that "static" pressure is also known as thermodynamic pressure.

I can see how a moving fluid impacting on a surface exerts a larger pressure than if the fluid was at rest. And if the impact area is parallel to the flow, the fluid molecules' should produce the same pressure that is produced when the fluid is not moving since the fluid molecule's momentum has not component perpendicular to the area surface...That is why I am led to believe that hydrostatic and "static" pressure should be the same...

Rather then spending your valuable time on terminology, why don’t you solve some practice problems. Once you do this, everything else will fall into place.

 

[fog37]

Ok. You may be right. Your questions was: "Is it possible to have static pressure in a horizontal system (where no elevation is involved and no connection to the atmosphere is involved)?"

Well, if we have a container in the shape of a horizontal cylinder, closed at both sides and full of water, the water will be at rest and the water pressure at point will be hydrostatic and the same in every direction. The kinetic term in Bernoulli's equation would be zero and we get the hydrostatic pressure.

But if one end of the container has a hole and the other end free to move and an external force is applied to it, the water will start flowing out of the hole and the pressure p inside the fluid will be different than the hydrostatic (from Bernoulli's equation). The pressure is not isotropic anymore and varies with direction. Conceptually, I don't see how the pressure measured on a small area parallel to the flow, at a certain depth, can be different from the pressure that exists when the water is at rest...

 

[Chestermiller]

Ok. You may be right. Your questions was: "Is it possible to have static pressure in a horizontal system (where no elevation is involved and no connection to the atmosphere is involved)?"

Well, if we have a container in the shape of a horizontal cylinder, closed at both sides and full of water, the water will be at rest and the water pressure at point will be hydrostatic and the same in every direction. The kinetic term in Bernoulli's equation would be zero and we get the hydrostatic pressure.

Are you saying that I can't pressurize that water in this closed container to a pressure substantially higher than atmospheric?

But if one end of the container has a hole and the other end free to move and an external force is applied to it, the water will start flowing out of the hole and the pressure p inside the fluid will be different than the hydrostatic (from Bernoulli's equation). The pressure is not isotropic anymore and varies with direction.

Pressure is always isotropic. That is part of the definition of pressure. It is the isotropic part of the stress tensor.

 

[fog37]

No, we can surely pressurize water to a pressure higher than atmospheric pressure. We just need to push on it.

I know that hydrostatic pressure is isotropic but it seems that in a moving fluid the pressure magnitude varies depending on the orientation of the infinitesimal area used to measure it which implies that it is not isotropic. I may be mistaken though.

 

[Chestermiller]

No, we can surely pressurize water to a pressure higher than atmospheric pressure. We just need to push on it.

I know that hydrostatic pressure is isotropic but it seems that in a moving fluid the pressure magnitude varies depending on the orientation of the infinitesimal area used to measure it which implies that it is not isotropic. I may be mistaken though.

You are mistaken. Only if the area stops the flow velocity will the measurement be higher. But that changes the flow that had existed. You are aware that you don’t have to have a solid surface present in order for (isotopic) pressure to exist, correct? The fluid parcels exert pressure on adjacent parcels even without a solid surface being present.

 

[Chestermiller]

When you block the flow with a pitot tube, you have not made the pressure non-isotopic. All you have done is increased the isotopic pressure to a higher value at the entrance to the pitot tube.

 

[fog37]

I see. Thank you.

What you are saying, if I understand it correctly, is that when we stop the moving fluid at a stagnation point, the pressure at that stagnation point is still isotropic (i.e. equal in all directions, like the pressure in a fluid at rest). If we "asked" the fluid particles around that stagnation point what pressure they experience, they would say the same pressure.

I agree that more practice would help sort out most of my doubts. I am having still having a conceptual hurdle about piezometric tubes. A piezometer (piezometric tube) is a vertical tube connected to the walls of a pipe with fluid inside.

• Apart from capillarity effects (if the diameter is too small), does the piezometer tube diameter matter? A piezometer measure the gauge pressure in the fluid right at its base (i.e. at the pipe walls). The vertical height reached by the fluid in the piezometer correlates with the pressure exerted by the fluid at the piezometer base. This liquid pressure at the piezometer base supports the liquid column inside the piezometer. This push (pressure) must be directed perpendicularly to the fluid flow.

• At the piezometer base, if the fluid is moving at a speed v, would the fluid pressure along the longitudinal direction (where the fluid is moving) be the same as the pressure measured transverse to the direction of flow that pushes the liquid up the piezometer? Based on the isotropy arguments above, it would.

• When a liquid is at rest, at a certain depth, the average random momentum of the fluid particles determines the pressure at that point. If the fluid was moving, how does the bulk fluid motion affect the pressure (average random fluid particle momentum) in a direction transverse to the bulk fluid motion?

 

[Chestermiller]

I see. Thank you.

What you are saying, if I understand it correctly, is that when we stop the moving fluid at a stagnation point, the pressure at that stagnation point is still isotropic (i.e. equal in all directions, like the pressure in a fluid at rest). If we "asked" the fluid particles around that stagnation point what pressure they experience, they would say the same pressure.

Yes, if, by particle, you mean parcel and not molecule.

Apart from capillarity effects (if the diameter is too small), does the piezometer tube diameter matter?

It does not matter as long as it doesn't encompass a lot of axial distance over which the pressure changes.

A piezometer measure the gauge pressure in the fluid right at its base (i.e. at the pipe walls). The vertical height reached by the fluid in the piezometer correlates with the pressure exerted by the fluid at the piezometer base. This liquid pressure at the piezometer base supports the liquid column inside the piezometer. This push (pressure) must be directed perpendicularly to the fluid flow.

The pressure at the base of the tube is the same in all directions. The tube must be oriented perpendicular to the fluid flow.

At the piezometer base, if the fluid is moving at a speed v, would the fluid pressure along the longitudinal direction (where the fluid is moving) be the same as the pressure measured transverse to the direction of flow that pushes the liquid up the piezometer? Based on the isotropy arguments above, it would.

Yes.

When a liquid is at rest, at a certain depth, the average random momentum of the fluid particles determines the pressure at that point. If the fluid was moving, how does the bulk fluid motion affect the pressure (average random fluid particle momentum) in a direction transverse to the bulk fluid motion?

From a frame of reference moving with the moving fluid velocity, the fluid is not moving. Either way, the pressure is isotropic. Repeat after me:

Pressure is isotropic
Pressure is isotropic
Pressure is isotropic

 

[fog37]

Thanks Chestermiller. I repeated "Pressure is isotropic" 40 times and I think I am getting it : )

Also, am I correct in thinking that:

at a hypothetical point A inside a fluid a certain depth $d$, the pressure is always isotropic. That pressure $P$ is larger if the fluid is at rest and smaller if the fluid is moving at speed $v$. The larger the speed $v$ the smaller that isotropic pressure will be.

Bernoulli's equation could be written this way: $$P= (constant)- \rho g d - \frac {1}{2} \rho v^2$$
which indicates that the larger $v$ the smaller $P$.

But we know that and the larger $d$ the higher $P$. The equation above instead shows that $P$ would decrease with depth $d$. That is clearly wrong...

Thanks!
fog32

 

[Chestermiller]

Thanks Chestermiller. I repeated "Pressure is isotropic" 40 times and I think I am getting it : )

Also, am I correct in thinking that:

at a hypothetical point A inside a fluid a certain depth $d$, the pressure is always isotropic. That pressure $P$ is larger if the fluid is at rest and smaller if the fluid is moving at speed $v$. The larger the speed $v$ the smaller that isotropic pressure will be.

You're trying to compare apples and oranges. For the same steady state flow, the pressure is smaller in higher speed regions than lower speed regions.

Bernoulli's equation could be written this way: $$P= (constant)- \rho g d - \frac {1}{2} \rho v^2$$
which indicates that the larger $v$ the smaller $P$.

But we know that and the larger $d$ the higher $P$. The equation above instead shows that $P$ would decrease with depth $d$. That is clearly wrong...

Thanks!
fog32

In the Bernoulli equation, the d in your equation should be elevation, not depth.

 

[fog37]

Ok. I see how, for the same steady state flow, the pressure is smaller in higher speed regions than lower speed regions. but if the flow was stopped, the pressure at those same point under examination in the fluid would be higher, I believe...

As far as $d$ being depth or elevation, when $v=0$, doesn't bernoulli's equation become the equation for hydrostatic pressure $$p = \rho g d$$ where $d$ is the depth in the liquid?

 

[Chestermiller]

Ok. I see how, for the same steady state flow, the pressure is smaller in higher speed regions than lower speed regions. but if the flow was stopped, the pressure at those same point under examination in the fluid would be higher, I believe...

If part of the flow is stopped, such as the tip of a pitot tube, then the pressure is higher there. But, if the entire flow is stopped, then the fluid is not moving at all at steady state, and you have a hydrostatic system.

As far as $d$ being depth or elevation, when $v=0$, doesn't bernoulli's equation become the equation for hydrostatic pressure $$p = \rho g d$$ where $d$ is the depth in the liquid?

Yes. That's why your equation in post #26 is wrong. It should read:
$$P+\rho g z = const.$$where z is measured upward (not downward).

 

[fog37]

1) I see how a fluid at rest and a fluid in steady motion are different situations. I guess I am wondering if the isotropic pressure, at the same spatial point in the liquid, would be higher if the fluid was at rest (not a stagnation point). How different would the pressure experienced by the liquid parcels be?

2) Ok, but if you take the equation in your post #29 (where $v=0$, which implies a fluid at reset) and move the term $\rho g z$ on the righthand side, we get the equation $$P=const. - \rho g z$$, which is what I have in my post #26 (different from the correct expression for hydrostatic pressure)...

 

[Chestermiller]

1) I see how a fluid at rest and a fluid in steady motion are different situations. I guess I am wondering if the isotropic pressure, at the same spatial point in the liquid, would be higher if the fluid was at rest (not a stagnation point). How different would the pressure experienced by the liquid parcels be?

Do you have a specific physical problem in mind that we can focus on (involving actual equipment and hardware)?

2) Ok, but if you take the equation in your post #29 (where $v=0$, which implies a fluid at reset) and move the term $\rho g z$ on the righthand side, we get the equation $$P=const. - \rho g z$$, which is what I have in my post #26 (different from the correct expression for hydrostatic pressure)...

That's not what you have in post #26. You have an h instead of a z. h is measured downwards and z is measured upwards. Do you not see the difference? If the datum for both elevation and depth is taken at the upper (free) surface of the fluid, then $h=-z$ and $p=-\rho g z = \rho g h$