dvolpe
- 34
- 0
Homework Statement
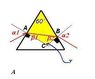
Equilateral triangle prism (angles all 60 degrees) made of crown glass. Index of refraction ranges from 1.486 for longest visible wavelengths to 1.556 for the shortest. What is range of refraction angles for the light transmitted into air through the right side of the prism?
Angle of white light entering prism is 55 degrees with respect to normal.
Homework Equations
n = [sin((60+D)/2)/(sin(60/2))]
The Attempt at a Solution
n min = 1.486 = sin ((60+D)/2)/[sin 30 deg)
1.486*.5 = sin (x)
x = (60+D)/2 = sin (.743)
(60+D)/2 = 47.987 or D = 35.974 degrees
This is WRONG! Help!