This sort of probability is a bit outside my usual comfort zone, but I'll have a go at it.
The length $\ell$ is immaterial, so I'll assume $\ell=1$.
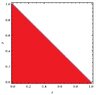
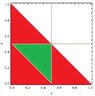
Suppose that the cuts occur at $y$ and $x$, with $x,\,y$ independently uniformly distributed in $[0,1]$ and $x$ denoting the larger of them. We must have $x\geqslant1/2$ if the three segments are to form a triangle (because none of the sides can be greater than $1/2$). So one side on the triangle has length $1-x$. The difference between the other two sides must be at most $1-x$, and so $y$ must lie in the interval $\bigl[x-\tfrac12,\tfrac12\bigr]$, of length $1-x$ (see the picture). The probability of that happening (for a given $x$) is $\frac{1-x}x$. However, the probability distribution of $x$ (as the maximum of the two cut points) is not uniform, but has p.d.f. $2x$. So the overall probability of the three segments forming a triangle is $$\int_{1/2}^1 \frac{1-x}x\,2x\,dx = \Bigl[2x-x^2\Bigr]_{1/2}^1 = 1-\frac34 = \frac14.$$
(I hope that's right!)