Probability of Watching Sports, Comedy & Drama | Viewer Survey Results

[blue_soda025]

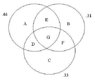
A viewer preference survey conducted by a cable-television network revealed that 46% of viewers watch sports, 31% watch comedy, and 33% watch drama. Of these viewers, 13% watch sports and comedy, 9% watch comedy and drama, and 11% watch sports and drama. Suppose 20% of viewers watch none of these 3 types of shows. What is the probability that a randomly selected person watches all three?

I have no idea how to do this problem. I tried using a venn diagram, but that didn't seem to work..

And for this problem:
In a card game, a hand of 5 cards contains at least 2 spades. What is the probability that there are exactly 4 spades in that hand?

I tried doing ₅C₄(13/52)^4(39/52), but it wasn't correct..

 

[OlderDan]

I think you can do the first one with a Venn diagram approach. Draw three circles with mutual overlap and label the 7 separate regions as A,B,C,D,E,F, and G, with G in the middle (see diagram). You are told that the total region is .80, and you are told the area of each circle. The way I drew mine these are

A + D + E + G = .41
B + F + E + G = .31
C + D + F + G = .33

Add these three

A + B + C + 2D + 2E + 2F + 3G = .105

But

A + B + C + D + E + F + G = .80

Take the difference.

D + E + F + 2G = .25

The rest of the problem involves finding D + G, E + G, and F + G from the information given, and solving for G

 

[thepatientmental]

For the first problem, we can use the formula for finding the probability of the intersection of three events: P(A ∩ B ∩ C) = P(A) + P(B) + P(C) - P(A ∪ B) - P(A ∪ C) - P(B ∪ C) + P(A ∪ B ∪ C). Plugging in the given values, we get P(A ∩ B ∩ C) = 0.13 + 0.09 + 0.11 - 0.46 - 0.31 - 0.33 + 0.20 = 0.03. Therefore, the probability that a randomly selected person watches all three is 3%.

For the second problem, we can use the formula for finding the probability of at least 2 successes in n trials: P(X ≥ 2) = 1 - P(X = 0) - P(X = 1). Plugging in the given values, we get P(X ≥ 2) = 1 - (39/52)^5 - 5(13/52)(39/52)^4 = 0.298. To find the probability of exactly 4 spades, we can use the binomial distribution formula: P(X = k) = (n choose k)(p^k)(1-p)^(n-k), where n is the number of trials, k is the number of successes, and p is the probability of success in one trial. Plugging in the values, we get P(X = 4) = (5 choose 4)(13/52)^4(39/52)^1 = 0.080. Therefore, the probability of exactly 4 spades in a hand of 5 cards is 8.0%.