thisischris
- 26
- 1
Hello everyone.. I'm stuck on this and don't really know what equations to apply or how you get the answer.
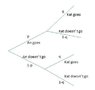
An and Kat go on each Friday to the cinema independently of each other. On any given Friday the probability of both going to the cinema is 1/3. And the probability that at least one of them goes is 5/6.
Find the possible values for the probability that An goes to the cinema on a Friday.
The answer at the back is 1/2 or 2/3.
Thank you!
An and Kat go on each Friday to the cinema independently of each other. On any given Friday the probability of both going to the cinema is 1/3. And the probability that at least one of them goes is 5/6.
Find the possible values for the probability that An goes to the cinema on a Friday.
The answer at the back is 1/2 or 2/3.
Thank you!