Problem in finding the radius of convergence of a series

[Amaelle]

Homework Statement

look at the image

Relevant Equations

asymptotic behaviour, raduis of convergence

Good day

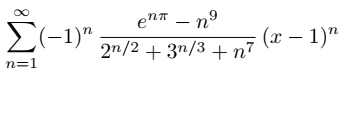
I'm trying to find the radius of this serie, and here is the solution

I just have problem understanding why 2^(n/2) is little o of 3^(n/3) ?

many thanks in advance

Best regards!

 

[BvU]

why 2^(n/2) is little o of 3^(n/3)

$$2^{n/2}= 1.4142^n \qquad 3^{n/3}= 1.4442^n \quad \Rightarrow \quad 2^{n/2} < 3^{n/3}$$

 

[anuttarasammyak]

$$[2^{n/2}+3^{n/3}+n^7]^{1/n}=3^{1/3}[1+k^n+\frac{n^7}{3^{n/3}}]^{1/n}$$
where
$$k=\frac{2^{1/2}}{3^{1/3}}$$
$$k^6=\frac{8}{9}<1$$
so k<1. As n$\rightarrow +\infty$
$$[1+k^n+\frac{n^7}{3^{n/3}}]^{1/n} \rightarrow 1$$

 

[Amaelle]

$$[2^{n/2}+3^{n/3}+n^7]^{1/n}=3^{1/3}[1+k^n+\frac{n^7}{3^{n/3}}]^{1/n}$$
where
$$k=\frac{2^{1/2}}{3^{1/3}}$$
$$k^6=\frac{8}{9}<1$$
so k<1. As n$\rightarrow +\infty$
$$[1+k^n+\frac{n^7}{3^{n/3}}]^{1/n} \rightarrow 1$$

So beautifully explained!, thanks a million!

 

[Amaelle]

$$2^{n/2}= 1.4142^n \qquad 3^{n/3}= 1.4442^n \quad \Rightarrow \quad 2^{n/2} < 3^{n/3}$$

Nice shot! thanks a million!