Amaelle
- 309
- 54
- Homework Statement
- look at the image
- Relevant Equations
- asymptotic behaviour, raduis of convergence
Good day
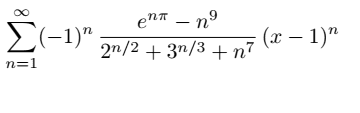
I'm trying to find the radius of this serie, and here is the solution

I just have problem understanding why 2^(n/2) is little o of 3^(n/3) ?
many thanks in advance
Best regards!
I'm trying to find the radius of this serie, and here is the solution
I just have problem understanding why 2^(n/2) is little o of 3^(n/3) ?
many thanks in advance
Best regards!