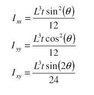emRage
- 5
- 0
Hi guys,
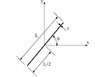
I would like to derive the Ixy equation from simple integration and I can't seem to get the right answer (third equation down the picture). I seem to be able to derive Ixx and Iyy easily but product moment of area requires first moment of area to be calculated and I just don't know how to do that on an inclined section.
Any help would be apprecited on this issue.
Thank you.
I would like to derive the Ixy equation from simple integration and I can't seem to get the right answer (third equation down the picture). I seem to be able to derive Ixx and Iyy easily but product moment of area requires first moment of area to be calculated and I just don't know how to do that on an inclined section.
Any help would be apprecited on this issue.
Thank you.