Sagrebella
- 61
- 2
Hello,
Could someone please check my answers to this physics problem? All my work and equations are clearly shown in the pictures below. If I got the problem wrong, please provide me with some suggestions as to how I can get it right . I'm not expecting anyone to just give me the answers :)
Thanks!
Problem 6
You flick a ball from a tabletop, so that the ball lands on the floor 1.50 m below. The ball's initial speed is 2.10 m/s. Use g = 9.80 m/s2.
(a) f the ball is launched off the table horizontally, what is the horizontal distance between the launch point and the point where the ball hits the floor?
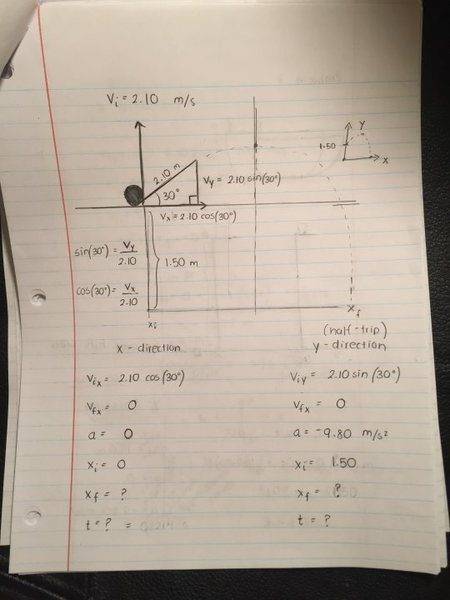
(b) If the ball is launched off the table at a 30° angle above the horizontal, what is the horizontal distance between the launch point and the point where the ball hits the floor?
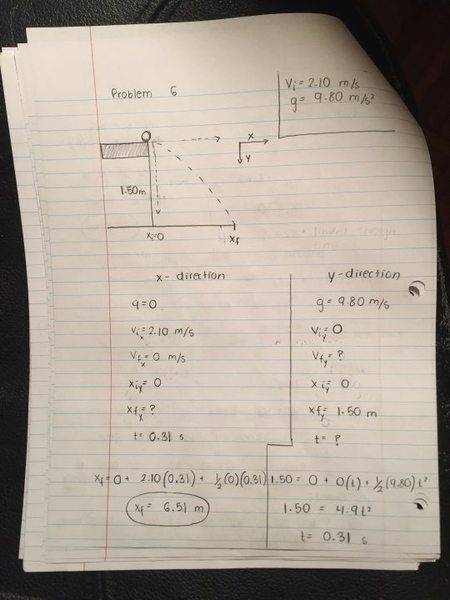
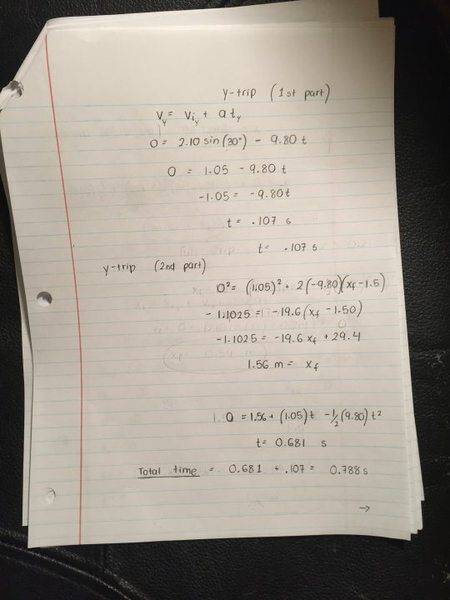
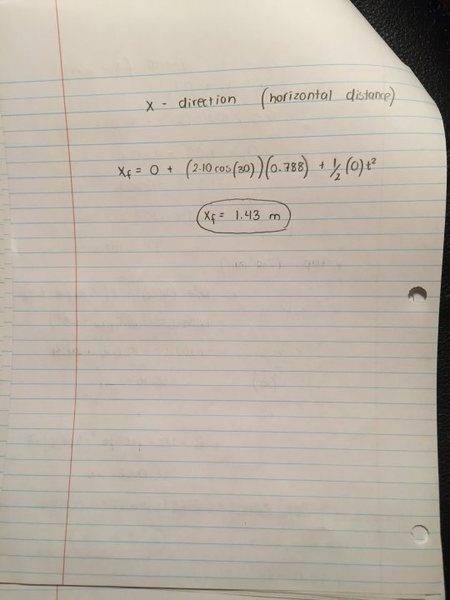
Could someone please check my answers to this physics problem? All my work and equations are clearly shown in the pictures below. If I got the problem wrong, please provide me with some suggestions as to how I can get it right . I'm not expecting anyone to just give me the answers :)
Thanks!
Problem 6
You flick a ball from a tabletop, so that the ball lands on the floor 1.50 m below. The ball's initial speed is 2.10 m/s. Use g = 9.80 m/s2.
(a) f the ball is launched off the table horizontally, what is the horizontal distance between the launch point and the point where the ball hits the floor?
(b) If the ball is launched off the table at a 30° angle above the horizontal, what is the horizontal distance between the launch point and the point where the ball hits the floor?