Projectile Motion Particle Problem

[moonbase]

Hello, I have a confusing problem here that I've spent a long time on today and can't seem to understand. I've found this on contextual problem websites so it's possible that one of you may have seen it before.

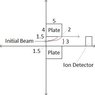
Also, ignore the graph I attached, I messed it up but it might give you an idea of how it's set up.

The scenario:
You have a summer job as an assistant in a university research group that is designing a devise to sample atmospheric pollution. In this device, it is useful to separate fast moving ions from slow moving ones. To do this the ions are brought into the device in a narrow beam so that all of the ions are going in the same direction. The ion beam then passes between two parallel metal plates. Each plate is 5.0 cm long, 4.0 cm wide and the two plates are separated by 3.0 cm. A high voltage is applied to the plates causing the ions between them to have a constant acceleration directly toward one of the plates and away from the other plate. Before the ions enter the gap between the plates, they are no longer accelerated during the 50 cm journey to the ion detector. Your boss asks you to calculate the magnitude of acceleration between the plates necessary to separate ions with a velocity of 100 m/s from those in the beam going 1000 m/s by 2.0 cm?

My take on it:
Either this problem is very poorly worded or I'm just not making sense of it. It is asking to find the acceleration needed to separate the ions by 2.0 cm, but I'm not sure if it's asking to separate them vertically or horizontally. Vertically wouldn't make sense because the ions start at the center of the 3.0 cm gap, leaving 1.5 cm for the streams to move (they can't move apart, must go in the same direction if I'm not mistaken), thus they could never become 2.0 cm apart vertically. However, horizontally separating them would not make sense either because the distance between them constantly changes and their horizontal velocity shouldn't change if the acceleration is going perpendicular to the streams' path ("acceleration directly toward one of the plates"). Also, I can't separate them by 2.0 cm in the z-axis because they are moving toward the plates, not apart from each other within the space between the plates. Sorry if what I said is confusing.

Sidenote: I'm also not sure whether the "50 cm journey" is the distance between the plates and the ion detector or the total distance covered. Another possible issue with this problem is whether the distance traveled through the plates is 4 cm or 5 cm depending on how they're positioned, but I'm assuming it's 5 cm.

Calculations:
So far I have time values for the period in which they're between the plates.

X-Components:

Slow Ions: x_f=0.05 m, x₀=0 m, v₀=100 m/s, a=0 m/s².
0.05=0+100t+0.5(0)t², 100t=0.05, t=0.0005 sec

Fast Ions: x_f=0.05 m, x₀=0 m, v₀=1000 m/s, a=0 m/s².
0.05=0+1000t+0.5(0)t², 1000t=5, t=0.00005 sec

Y-Components:

Slow Ions: y_f=0.03 cm, y₀=0.015 cm, v₀=0 cm/s, t=0.0005 sec.
0.03=0.015+0(0.0005)+0.5a(0.0005)², 0.000000125a=0.015, a=120000 m/s²

Fast Ions: y_f=0.03 cm, y₀=0.015 cm, v₀=0 cm/s, t=0.00005 sec.
0.03=0.015+0(0.00005)+0.5a(0.00005)², 0.00000000125a=0.015, a=120000000 m/s²

So I've apparently found the accelerations required to move the ions to the plate's surface by the time they leave the gap, but now I'm confused as to what I do with them because all they do from this point on is move toward the detector without the force acting on them. Can anyone help?

 

[Simon Bridge]

Welcome to PF.
Your diagram is not what the boss is asking - sure some slow-moving ions will impact the plates like you show, but you want them to impact the detector. So you want the 100-1000m/s ions to leave the area between the plates without hitting the plates.

When they do they will be traveling at an angle to horizontal which depends on their speed. This translates into a vertical displacement by the time they hit the detector.

 

[moonbase]

Ahhhh, I see. Thank you!