powerof
- 43
- 0
Homework Statement
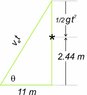
A soccer player is taking a penalty kick from a distance of 11 meters from a goal which is 2.44 m high (forgive the possible incorrect use of English, since I'm not a native speaker). Given an initial speed of the ball of 90 km/h (which is 25 m/s2) calculate the initial upward angle of the ball for it to hit the upper bar (i.e., have height = 2.44 after having traveled 11 m horizontally).
Homework Equations
The trajectory equation for x_0=y_0=0 (initial horizontal and vertical positions) is:
y = (tan\theta)x - (\frac{g}{2(v_0)^2 cos^2 \theta})x^2
Some known constants in the above equation are:
v_0=25 m/s \ \ \ \ \ \ g = 9.81 m/s^2
And obviously \theta\in(0,\frac{\pi}{2})
The Attempt at a Solution
The straightforward way is to just substitute the known data in the main equation and solve for \theta:
2.44 = 11(tan\theta) - (\frac{9.81}{2(25)^2 cos^2\theta})11^2
But I'm lazy and I find solving for theta to be long and tedious (for me at least) so what I'm asking is:
Are there are any other ways for finding the angle in the mentioned problem besides the classic method I gave you?
I feel it's a long shot but I'm in no hurry and it doesn't hurt to ask. Also it doesn't necessarily have to be an easier method. Just post any you can think of.
Thanks for reading this and hopefully answering it.
Have a nice day!