kdf8
- 2
- 0
Okay, I'm in a rut. We got a pack of physics problems from our teacher and no one knows how to go about doing them and he refuses to help us. This is the first one I've ran into major trouble with.
Here's the problem:
An enemy ship is on the east side of a mountainous island, as shown in the figure below. The enemy ship can maneuver to within 2500 m of the 1800 m high mountain peak and can shoot projectiles with an initial speed of 250 m/s. If the western shoreline is horizontally 300 m from the peak, what are the distances from the western shore at which a ship can be safe from the bombardment of the enemy ship?
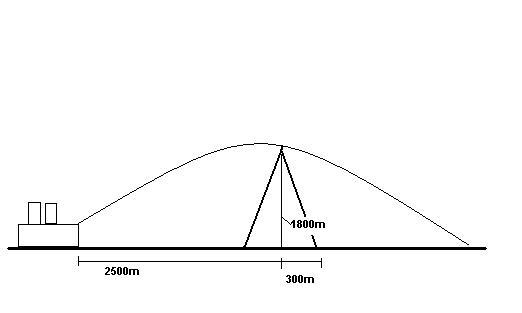
Sorry for such a rough hand sketch, I don't have a scanner.
I've tried working out this problem from doing my own research on projectile motion and basically I know I need to find the smallest and largest angles that will clear the mountain peak and find where those angles will cause the projectile to land, but I have no idea how to do that, equation wise. ANY help will be greatly appreciated.
Here's the problem:
An enemy ship is on the east side of a mountainous island, as shown in the figure below. The enemy ship can maneuver to within 2500 m of the 1800 m high mountain peak and can shoot projectiles with an initial speed of 250 m/s. If the western shoreline is horizontally 300 m from the peak, what are the distances from the western shore at which a ship can be safe from the bombardment of the enemy ship?
Sorry for such a rough hand sketch, I don't have a scanner.
I've tried working out this problem from doing my own research on projectile motion and basically I know I need to find the smallest and largest angles that will clear the mountain peak and find where those angles will cause the projectile to land, but I have no idea how to do that, equation wise. ANY help will be greatly appreciated.